Существенной характеристикой сложного поведения нелинейных систем является ляпуновский показатель. Проще всего его ввести для дискретных отображений. Ляпуновский показатель характеризует поведение двух изначально очень близких точек в фазовом пространстве. С течением времени расстояние между ними меняется экспоненциальным образом, как раз с величиной показателя. Поэтому если он отрицателен, то точки сближаются, и мы имеем периодический режим. Если же показатель положителен, то точки расходятся. Таким образом, ляпуновский показатель является мерой присущей системе чувствительной зависимости от начальных условий и может тестировать хаос.
Для отображений число ляпуновских показателей в системе равно размерности фазового пространства. При этом, если один показатель положителен, то имеем хаос, если два – то гиперхаос.
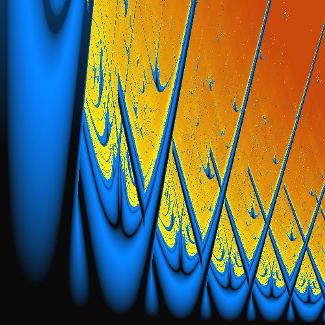
Весьма информативным является представление ляпуновского показателя на плоскости параметров системы, когда каждая точка окрашивается в свой цвет, определяемый величиной показателя. На представленном примере градациями синего цвета отмечены области отрицательного показателя («моря»), а оттенками красного и желтого – положительного («суша»). На рисунке показана ляпуновская карта старшего ляпуновского показателя для отображения Икеды.

Для автономных систем с непрерывным временем периодические орбиты характеризуются присутствием нулевого показателя (отвечающего возмущению типа сдвига вдоль траектории), однако, при построении карт его целесообразно исключить и рассматривать зависимость от параметров наибольшего из ненулевых показателей. Тогда соответствие между типом режима и знаком показателя Ляпунова такое же, как и для отображений.
Карты ляпуновских показателей для других систем можно посмотреть,
открыв атлас карт ляпуновских показателей.
К предыдущей странице Вернуться в оглавление К следующей странице