Автор: доктор физико-математических наук, профессор

1 1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1 1 6 15 20 15 6 1 1 7 21 35 35 21 7 1 .....................
Треугольник Паскаля	Доска Гальтона

Рассмотрим последовательность x0, x1, x2, …, получаемую по правилу: xn+1=A-xn2, где A – постоянное число (параметр). При A<0,75 она сходится к неподвижной точке; в интервале от 0,75 до 1,25 – к циклу периода 2; от 1,25 до 1,368 – к циклу периода 4, затем имеются уменьшающиеся интервалы, где возникают циклы периода 8, 16, 32,… При переходе через A=1,401155189… возникает сложная динамика:
существует множество значений параметра, для которых реализуется хаос и множество, для которого имеет место периодическое поведение. Аналогичный сценарий перехода к хаосу наблюдается в системах разной физической природы (нелинейный маятник с затуханием под периодическим воздействием, конвекция в слое жидкости и др.)

Подвесьте грузик на нитку и качните его. Это маятник – один из самых простых и глубоких объектов исследования в физике, математике, теории колебаний.

1957 г. – запуск в СССР первого спутника, 1959 г. – первая фотография обратной стороны Луны, 1961 г. – первый полет человека – Ю.А.Гагарина в космос. Первый полет на Луну – Н.Армстронг и Дж.Олдрин. Космические корабли СССР-России: Восток, Восход, Союз, Буран, и США: Меркурий, Джемини, Аполло, Спейс-Шаттл. Орбитальные станции “Салют”, “Скайлэб”, “Мир”, МКС.

Медленное течение вязкой жидкости ламинарное, быстрое, бурлящее течение в ручье – турбулентное. Что известно о причинах возникновения турбулентности, какие подходы разработаны и применяются для ее исследования?

В школе изучают планиметрию – геометрию на плоскости и стереометрию – геометрию в пространстве. Вообразим себе мир, в котором кроме длины, ширины и высоты есть еще одно измерение. Это четырехмерный мир – математическая абстракция, но обладающая особой наглядностью и красотой.

Развертка четырехмерного куба	Каркас четырехмерного куба: “вид сверху”

Представим себе частицу, которая движется, скажем, на плоскости, совершая маленькие шаги один за другим в направлении, выбранном случайным образом. Это модель броуновского движения – движения частицы под действием хаотических толчков молекул окружающей среды.

Арифметическая прогрессия: 4, 7, 10, 13, 16, … Геометрическая прогрессия: 2, 6, 18, 54, 162, … Числа Фибоначчи: 1, 1, 2, 3, 5, 8, 13, 21, 34,…

“Треугольные числа”

“Золотое среднее”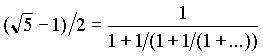

Год=365,242196 суток=

Периодическая последовательность: 011011011011011011…

Случайная последовательность: 01100010111010…

Непериодическая, но регулярная последовательность Морса-Туэ: последовательность сумм цифр последовательных двоичных чисел: четное 0, нечетное 1: 0110100110010110… Правило: начните с 0 и делайте раз за разом подстановку 0¬ 01, 1¬ 10. Результатом будет МТ-последовательность!

Последовательность кроликов (подстановка 0¬ 1, 1¬ 10): 10110101…

Фракталы – это образования в природе (береговые линии, горные массивы, вихри вихревая структура турбулентной жидкости) или геометрические объекты в математике, которые демонстрируют точное или приближенное подобие своих частей целому.
Снежинка Коха	Салфетка Серпиньского	Множество Мандельброта

	Пусть мы имеем возможность управлять состоянием какой-то системы, изменяя один, два или более параметров. Пример – изображенная на рисунке “качалка”, в которой управляющие параметры – координаты грузика, показанного красным кружком.
При выходе из желтой области происходит “катастрофа” - скачкообразное изменение состояния. Теория катастроф – математическая дисциплина, которая коллекционирует, описывает, анализирует и классифицирует такого рода переходы. С математической точки зрения, это далеко идущее обобщение исследования на максимум и минимум для функций, зависящих от нескольких переменных и параметров.

Выдающийся советский физик Петр Леонидович Капица (1894-1984). Лауреат Нобелевской премии за экспериментальные работы в области физики низких температур (1978). Создатель Института физпроблем. Один из главных организаторов МФТИ. Автор знаменитых "Задач Капицы".

Выдающийся советский физик Лев Давидович Ландау (1908-1968). Лауреат Нобелевской премии за работы в области квантовой теории конденсированных сред (1962). Автор многотомного Курса теоретической физики (с Е.М.Лифшицем). Создатель научной школы теоретической физики. "Теорминимум Ландау".

Выдающийся американский физик Ричард Фейнман (1928-1986). Лауреат Нобелевской премии за работы в области квантовой электродинамики (1965). Один из интереснейших персонажей в физике ХХ века. Автор популярнейшего курса “Фейнмановские лекции по физике”. Автор книги "Вы, конечно, шутите, мистер Фейнман!" (Surely, You're Joking, Mr. Feynman!).

Изготовьте два маятника, связанные пружиной и понаблюдайте за их колебаниями. Две колебательные моды: навстречу – период меньше, в одну сторону – период больше. Биения: толкните один маятник, когда второй в покое и посмотрите, что будет. Энергия периодически перекачивается от одного к другому и обратно!

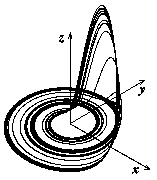
Рассмотрим систему, состояние которой задается N переменными, и представим изменение состояния во времени как движение изображающей точки по соответствующей траектории в N-мерном пространстве. Установившиеся режимы периодических колебаний изображаются замкнутыми орбитами – предельными циклами, квазипериодические колебания – торами, хаос – ? Странными аттракторами!

Предельный цикл	Тор	Странный аттрактор

А - 62	Б - 14	В - 38	Г - 13	Д - 25	Е - 72	Ж - 7	З - 16
И - 62	К - 10	Л - 28	М - 26	Н - 53	О - 90	П - 23	Р - 40
С - 45	Т - 53	У - 21	Ф - 2	Х - 9	Ц - 4	Ч - 12	Ш - 6
Щ - 3	Ь,Ъ 14	Ы - 16	Э - 3	Ю - 6	Я - 18	пробел	- 175