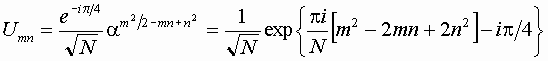As mentioned, constructing the operator map we face a necessity of selection - to set K'=KA or AK. Both forms are compatible with the classic map but are not equivalent due to non-commutativity of the operators: they differ by factor a, as KA=aAK. Let us consider an "intermediate" variant K'=a^1/2KA=a^-1/2AK. For the second equation let us keep the symmetric form: A'=AKA.

Substitute expressions for the matrix elements K_mn=d_m+1,n and A_mn=a^md_mn into the operator map K'=a^1/2KA, A'=AKA and estimate the matrix products. The result is K'_mn=d_m+1,na^n-1/2, A'_mn=a^m+nd_m,n-1.

Let us pass now to the Schrodinger representation and find the matrix of the evolution operator U. As we have UK'=KU, we obtain U_m,n-1a^n-1/2=U_m+1,n. Analogously, the condition UA'=AU yields U_m,n-1a^2n-m-1=U_mn. As follows from the first expression, the diagonal elements satisfy U_m+1,m+1=U_mma^m+1/2, so

Next, with a use of the second expression we have

.

It is easy to check that the resulting expression for U_mn has the correct period N in respect to both indices. Let us select the initial element as U₀₀=N ^-1/2e^-ip/4. Then, |DetU|=1, and the trace of the matrix appears to be real positive. Finally, we obtain