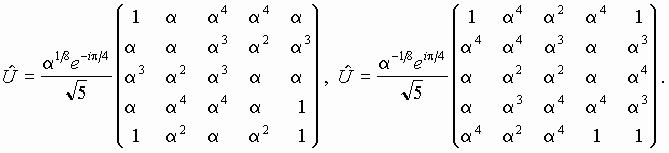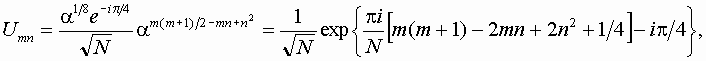
In the Heisenberg representation, the shift operators K and A evolve in time: at the next step we have K'=KA, A'=AKA. Let |y> be some state vector. Let us try to construct such an unitary operator U to have in the space of transformed vectors |y'>=U|y> the operators K' and A' equal to original ones, i.e. UK'U^-1=K, UA'U^-1=A. This is a passage to the Schrodinger representation: a state vector is regarded as evolving in time in accordance with the equation |y'>=U|y>, while the operators K and A are fixed. From the above expression it follows that UK'=KU, UA'=AU, or, in the matrix form, accounting the postulated form of the shift operators

U_m+1,n+1=U_mnaⁿ⁺¹, U_m,n+1=U_mna^2n-m+1.

Departing from the matrix element U₀₀, we obtain step by step the diagonal elements from the first equation: U_m+1,m+1=U_mma^m+1, i.e. U_m,m=U₀₀a^m(m+1)/2. Next, knowing one element in each row, with the second equation obtain the elements of the whole row: U_m,n=U₀₀a^{m(m+1)/2-n(m-n)}.

To make the operator U unitary, we select U₀₀ in such way that |detU|=1. It may be shown that this is ensured if |U₀₀|=1/N^1/2. The phase factor may be arbitrary as it does not effect on the observable values (it determines only the origin for quasienergy). Nevertheless, it is convenient to concretize it to have the trace of the matrix equal to real positive number. Thus,

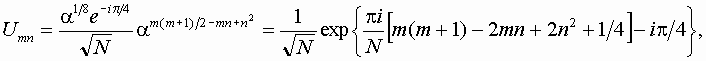
причем detU=1 и TrU=1. В частности, для N=5