|
|
|
Coupled map lattices: The lattice scaling
Let us consider a set of maps arranged into a spatial lattice (one- two- or three-dimensional) with a pairwise coupling between the cells. It is assumed that the system possesses the translation invariance, i.e. a spatial shift changes nothing, all the cells and the bonds are identical.
One of the intrinsic properties of the coupled map lattices is a possibility of formation of domain patterns. Let us imagine first a lattice without coupling, and let the control parameter is of such value that all the cells demonstrate the period-2 stable cycle. By selection of initial conditions for the lattice we can obtain a large number of states. Indeed, at any moment of time each cell can be in two possible states associated with two points of the period-2 orbit of the individual map. These states also will exist in presence of coupling at least while its strength is sufficiently small.
|
|
|
A part of lattice, where the neighboring cells are instantaneously in the same state (with coupling it is better to say in close states), is called a domain. Borders between the domains are the domain walls. Considering situations when the cells demonstrate period 4 or 8 one can see that the number of possible states essentially increases. Moreover, the domains can have hierarchical structure: domains of the first level, inside them there may be domains of the second level etc.
In the case of weak coupling the same scaling regularities are valid for the lattices as in the two coupled maps. Model map is constructed by introducing pairwise inertial and dissipative coupling between the neighboring cells. For example, for the one-dimensional lattice it is the equation
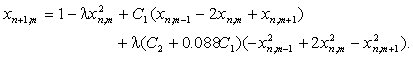
and for two-dimensional it is
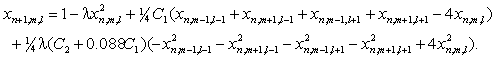
The property of lattice scaling consists in the following. Selecting the parameter values(D l / d , C
1/ a, C2/2) we can observe similar dynamical regimes as those at (D l , C1, C2), but with the doubled time scale. Note that initial conditions for all maps constituting the lattice must be rescaled by factor a=-2.5029. Here d =4.6692 û is the Feigenbaum constant, D l= l - l c, l c=1.4011552...For a one-dimensional lattice with pure dissipative coupling Kaneko has plotted a phase diagram in the parameter plane shown in the following figure. Areas of different regimes, or phases, are distinguished there:
FRP, PS, PCI, BD, DT, FDT. The property of lattice scaling implies that the analogous structure has to take place inside the smaller rectangular (with scale change by d along the horizontal, and by 2 along the vertical axis), if one uses the initial conditions of amplitude decreased by factor a. This is indeed the case, see the presented illustrations, the space-time diagrams for dynamics of the Kaneko phases inside the small rectangular.|
|
|
|
The next figure depicts the space-time diagrams. The horizontal is the space coordinate, and the vertical (from top to bottom) is time. Black or white color implies that the corresponding values of the dynamical variable are either larger, or less then the fixed-point value in the individual map. Note that the states are shown at each 4-th step of iterations. |
|
|
|
To illustrate domain patterns and their lattice scaling we present in the next figure the spatial diagrams for the lattice with dissipative coupling. Each plot shows a set of states relating to several subsequent steps of time. It may be seen from the picture, what are the rules of the scale changes associated with the property of the lattice scaling. |
|
|
|
Finally, let us turn to the one-dimensional lattice with pure inertial coupling
In the following figure the central diagram is the chart of regimes in the parameter plane. Two pairs of spatial diagrams in the top and in the bottom parts of the figure, respectively, show regimes similar in the sense of lattice scaling. |
|
|
Saratov group