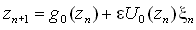
Путь имеем комплексное аналитическое отображение, отвечающее критической точке накопления бифуркаций утроения периода, с добавленным случайным воздействием:

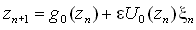
где

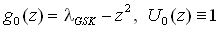
и x_n - последовательность статистически независимых комплексных случайных величин с нулевым средним и фиксированным среднеквадратичным значением s.

Применим это отображение трижды. Полагая параметр интенсивности шума e малым, в первом порядке по этому параметру получаем:

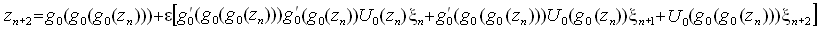
или после масштабной замены x-->x/a, используя комплексную масштабную константу Гольберга – Синая – Ханина a=–2.09691989+2.35827964i, получаем

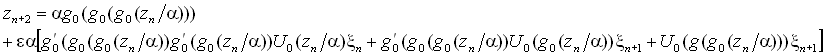
Фигурирующее с коэффициентом e выражение будем интерпретировать как новую случайную величину, и обозначим ее как U₁(z_n)x'_n, причем множитель U₁(z_n)x'_n вводим так, чтобы величина x'_n имела такое же среднеквадратичное отклонение s как и исходная случайная последовательность x. Поскольку x_n, x_n+1, x_n+2 статистически независимы, среднеквадратичные значения членов суммы по модулю складываются. Тем самым, уравнение для трехкратной итерации мы свели к такому же виду, как исходное, а именно,

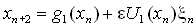
но с новыми функциями

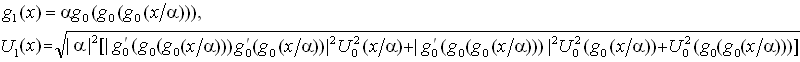
Проведенное преобразование можно применить многократно, что дает последовательность функций g_k, U_k, удовлетворяющих цепочке рекуррентных функциональных уравнений. Последовательность g_k стремится к пределу – неподвижной точке функционального ураувнения Гольберга – Синая – Ханина

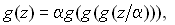
решение которого известно (получено численно в виде полиномиальной аппроксимации функции g(z), см. здесь).

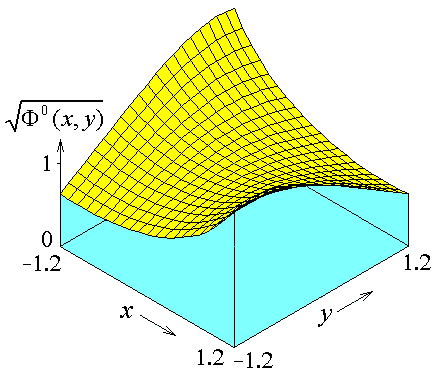
Решение для U_k можно искать в виде |U_k(z)|²µg^kФ(z), что приводит к задаче на собственные функции и собственные значения

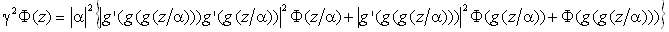
Заметим, что здесь фигурирует действительная функция комплексного аргумента Ф(z) и действительное собственное число g.

Согласно результатам численных расчетов, g=12.2066409. График соответствующей собственной функции показан на рисунке.