Влияние шума в точке окончания линии бифуркации удвоения тора

Рассмотрим систему, способную демонстрировать каскад бифуркаций удвоения периода и находящуюся под действием квазипериодически изменяющейся во времени внешней силы. Подходящая модель - логистическое отображение с дополнительным членом, описывающим внешнее воздействие:

Соотношение частот внешнего воздействия и собственного ритма отсчетов дискретного времени считается равным "золотому среднему". На плоскости параметров системы (l, e) имеется так называемая линия бифуркации удвоения тора, которая начинается в точке l=0.75, e=0 и тянется при увеличении e до точки своего окончания - критической точки TDT (Torus Doubling Terminal), расположенной при l_c=1.158096856726, e_c=0.360248020507.

Ренормгрупповой (РГ) анализ динамики в точке TDT был развит в работе [Kuznetsov, Pikovsky and Feudel, 1988]. Критическое поведение в точке TDT и различные динамические режимы характерные для ее окрестности наблюдались в эксперименте с нелинейным колебательным контуром при квазипериодическом воздействии [Bezruchko, Kuznetsov and Seleznev, 2000]. Поскольку в реальных физических системах неизбежно присутствует шум, представляет интерес рассмотреть его воздействие на динамику в точке TDT. Обратимся к модели, в которой добавлен стохастический член:

Здесь x_n - последовательность статистически независимых случайных величин с нулевым средним и фиксированным среднеквадратичным значением s, k - параметр, характеризующий интенсивность шума, который считается малым.

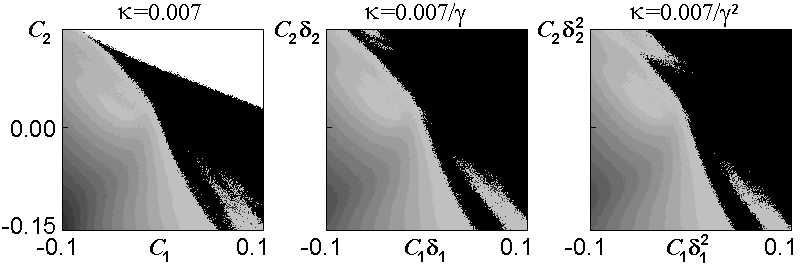
Ниже показаны карты показателя Ляпунова на плоскости параметров (l, e) без шума (первая диаграмма) и в присутствии шума при k=0.03 (вторая диаграмма). На первой карте отмечено положение точки TDT и приведены надписи, поясняющие тип режимов: гладкие тор-аттракторы T1 и T2, странный нехаотический аттрактор SNA, хаос. При построении карты для каждого элемента графического изображения, отвечающего определенным l и e, вычисляется показатель Ляпунова, и соответствующий пиксель кодируется тонами от темного к светлому для значений показателя от минус бесконечности до нуля, и черным для положительных значений.

В присутствии шума картина характерных областей на картах показателя Ляпунова остается видна, но ее тонкие детали картины оказываются "замазаны".

На следующем рисунке представлены фазовые портреты аттракторов при значениях l и e, отыечающих кратической точке, на итерационных диаграммах - на графиках зависимости x_n+1 от x_n. Первая диаграмма построена без шума, вторая и третья в присутствии шума, при указанных на рисунках значениях параметра k.

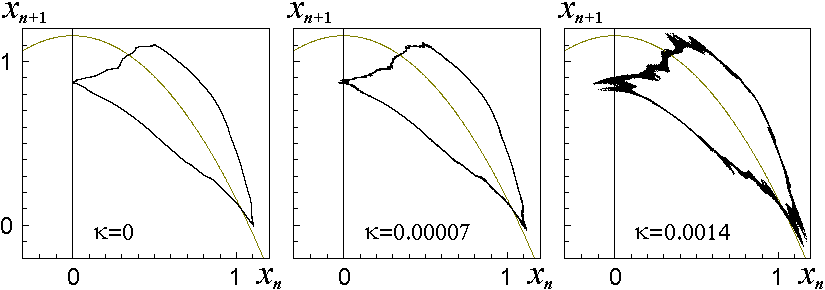
Можно видеть, как с увеличением шума последовательно размываются сначала тонкие, а затем более крупные детали структуры аттрактора.

Поскольку без шума вблизи точки TDT имеют место определенные закономерности скейлинга, можно полагать, что и воздействие шума должно характеризоваться какими-то свойствами скейлинга.

Ренормгрупповой анализ задачи с шумом приводит к заключению, что для наблюдения каждого следующего уровня связанной с точкой TDT мелкомасштабной структуры (что соответствует увеличению характерного временного масштаба в W³=4.236068... раз) амплитуда шума должна быть уменьшена на фактор g=20.048637712.

Для более аккуратной формулировки свойства скейлинга целесообразно ввести на плоскости параметров специальную локальную систему координат, которая, согласно численным расчетам, для нашей модели может быть определена соотношениями

Предположим, что вблизи точки TDT в присутствии шума уровня k наблюдается некоторый режим при значениях параметров l и e, которым отвечают локальные координаты c₁ и c₂. Тогда при значениях параметров, соответствующих c₁/d₁ и c₁/d₂, где d₁=10.5029835, и d₂=5.1881181, и уровне шума e/g будет реализоваться статистически подобный режим поведения с характерным временным масштабом в W³=[(5^1/2+1)/2]³ раз большим. При этом закон распределения переменной x вблизи экстремума x=0 будет подобен исходному, с характерным масштабом по x в a=3.96376656 раз меньше. В области малых отклонений от критичности и малом уровне шума закон распределения, как можно полагать, в значительной мере универсален, т.е. не зависит от деталей распределения и корреляционных свойств исходного шума (лишь бы функция корреляции убывала достаточно быстро).

Рассмотрим несколько компьютерных иллюстраций указанного свойства скейлинга.

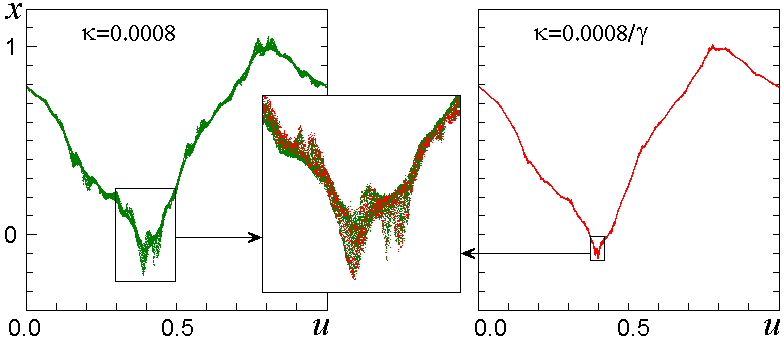
Начнем с графиков, на которых изображен "зашумленный" аттрактор в координатах u, x. На второй картинке уровень шума в g раз меньше, чем на первой. Значения параметров l и e отвечают критической точке TDT. На каждой диаграмме выделен фрагмент, воспроизведенный на вставке в центре, причем фактор увеличения для второго аттрактора больше в a раз по оси x и в W₃ раз по оси u. Хорошее соответствие наложенных на одном графике "красного" и "зеленого" объектов иллюстрирует свойство скейлинга в системе с шумом.

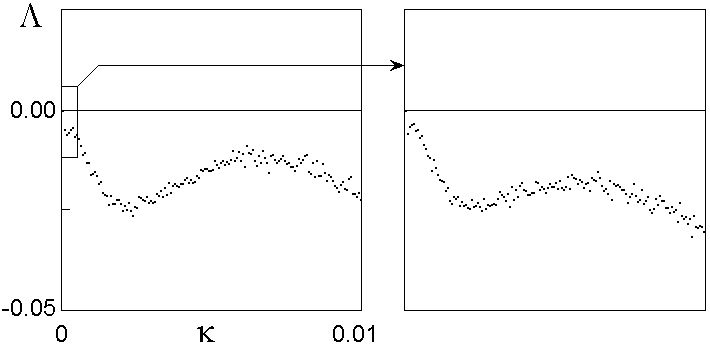
Обратимся теперь к диаграммам, показывающим зависимость показателя Ляпунова от интенсивности шума при значениях параметров l и e, соответствующих точке TDT. Из рисунка видно, что включение шума приводит к уменьшению показателя Ляпунова, т.е. способствует стабилизации (в противоположность тому, что имеет место для перехода по Фейгенбауму, когда присутствие шума способствует увеличению показателя Ляпунова). На вставке показан фрагмент графика с пересчетом масштаба по горизонтали на фактор g, а по вертикали - в W³ раз. Сходство обеих картинок служит проявлением ожидаемого свойства скейлинга.

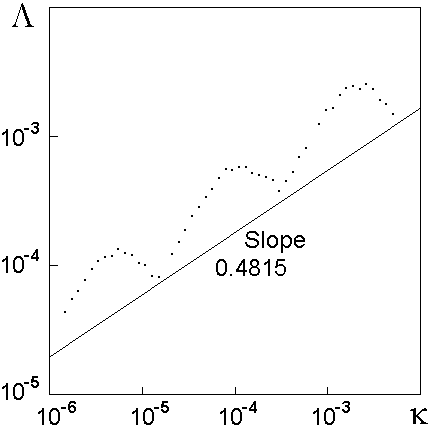
Другой способ продемонстрировать свойство скейлинга состоит в том, чтобы представить результаты расчета показателя Ляпунова в зависимости от уровня шума в двойном логарифмическом масштабе. Из графика видно, что точки располагаются в среднем вдоль наклонной прямой с угловым коэффициентом log_gW³=0.4815.

Следующая серия иллюстраций - ляпуновские карты на плоскости параметров, относящиеся к малой окрестности критической точки TDT и построенные в "скейлинговых координатах". Тона серого цвета от темных к светлым кодируют уровень показателя Ляпунова от минус бесконечности до нуля, а черный цвет соответствует положительным значениям показателя. При переходе к каждой последующей картинке для иллюстрации скейлинга масштаб по горизонтали и вертикали пересчитывается на факторы, соответственно, d₁ и d₂, а уровень шума уменьшается в g раз. Кроме того, переопределяется правило кодирования величины показателя Ляпунова серыми тонами с тем, чтобы учесть изменение характерного временного масштаба динамики на фактор W³.

• Действие шума на фейгенбаумовский тип поведения
• Действие шума при переходе к хаосу через квазипериодический режим с отношением частот "золотое среднее"
• Действие шума на критическое поведение, связанное с утроениями периода
• Влияние шума на критическое поведение модели с квазипериодическим воздействием в точке окончания линии бифуркации удвоения тора