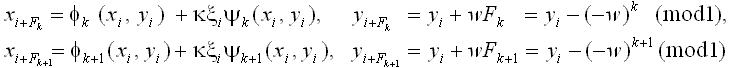
В применении ко всем ситуациям квазипериодического движения с числом вращения золотое среднее, главная идея РГ анализа состоит в исследовании операторов эволюции, определенных для интервалов времени, заданных последовательными числами Фибоначчи: F_k+1=F_k+F_k-1, F₀=0, F₁=1. Предположим, что в присутствии шума эволюция пары переменных x и y в точке TDT для F_k и F_k+1 шагов задается уравнениями

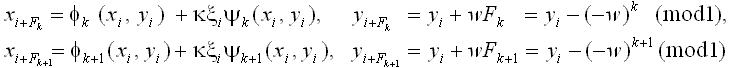
где x_n - последовательность статистически независимых случайных величин с нулевым средним и фиксированным среднеквадратичным значением s, k - параметр, характеризующий интенсивность шума, который считается малым, y_n(x) и y_n+1(x) - вспомогательные функции. Ясно, что модельное отображение, представленное в основном тексте, можно рассматривать как частный случай: при F₁=F₂=1 полагаем

Применяя последовательно отображения, отвечающие F_k+1 и F_k шагам, и учитывая члены первого порядка по амплитуде шума k получаем для числа шагов F_k+2 стохастическое отображение

.

Переопределим стохастический член. Предположим, что в некоторый момент орбита стартует из точки (x_i, y_i). Рассмотрим ансамбль случайных чисел {x_i, x_i+Fk+1} с нулевым средним и дисперсией s² и составим сумму с коэффициентами, заданными функциями x_i и y_i. Поскольку члены суммы статистически независимы, ее можно представить опять же как случайное число с нулевым средним и дисперсией s², умноженное на функцию x_i и y_i:

Введем теперь

и перепишем уравнение в форме, аналогичной исходной, с переопределенной случайной переменной и функциями f и y:

Чтобы получить замкнутую систему функциональных уравнений, возведем обе части полученного уравнения в квадрат и выполним усреднение по ансамблю реализаций с шумом. Поскольку

приходим к соотношению

где штрих означает производную по первому аргументу. Следуя основной идее ренормгруппового подхода, произведем пересчет масштаба,

где a - константа перенормировки, найденная ранее для критической точки TDT. Тогда в терминах функций переопределенных с изменением масштаба

приведенные выше уравнения означают, что

Эти соотношения определяют ренормпреобразование для набора функций {g_k, f_k, Y_k, F_k}. Процедура может быть повторена снова и снова, чтобы получить функции для все больших k, то есть определить перенормированные операторы эволюции на интервалах, заданных количеством шагов дискретного времени F_k.

Известно, что в критической точке TDT последовательность функций g_k, f_k сходится к стационарному решению периода 3, определяемому уравнениями

или

Сходимость функций g_k, f_k к решению в виде цикла периода 3 подразумевает, что рекурсивные линейные функциональные уравнения для функциональных пар {Y_k, F_k} в асимптотике будут определяться собственным вектором, связанным с наибольшим собственным значением W для следующей задачи на собственные значения

где присутствующие в правой части линейные операторы выражаются как

Численное решение этой задачи приводит к результату W=401.94787411... Теперь в линейном приближении по отношению к амплитуде шума, стохастическое отображение, отвечающее F₃k+q и F₃k+q+1+1 шагам эволюции в критической точке TDT может быть записано в ренормализованных переменных как

где

Учитывая дополнительно возмущения оператора эволюции, вызванные смещением по параметрам из критической точки, отсюда можно вывести формулировку закона подобия, приведенную в основном тексте.
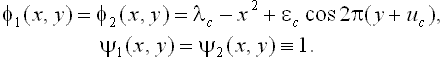
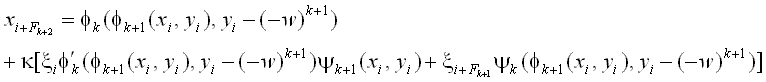
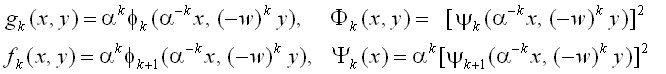
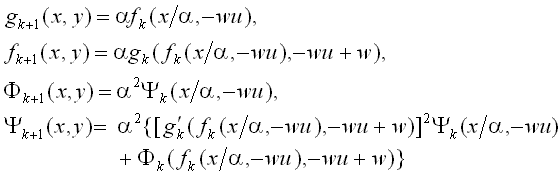
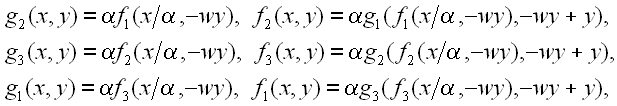
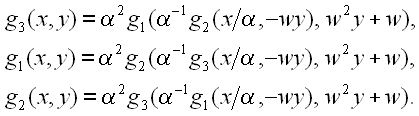
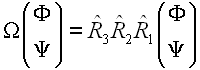
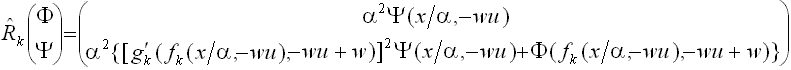
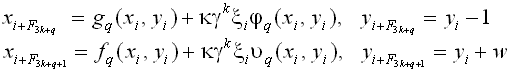