Отображение Эно

Простейшим одномерным отображением со сложной динамикой является логистическое отображение

или ,

которое описывает, например, динамику популяции.

В предыдущем разделе на примере задачи о прыгающем шарике мы познакомились с двумерными отображениями. Нельзя ли построит двумерное обобщение логистического отображения? Оказывается, можно. При введении одномерного отображения мы предполагали, что численность популяции в (n+1)-ый год зависит лишь от численности в n-ый год. Предположим теперь, что память "глубже" - численность в (n+1)-ый год зависит и от численности в (n-1)-ом году. Эта зависимость должна быть слабой. Поэтому будем полагать ее линейной. Тогда

,

где b - некоторый новый коэффициент.

Введем теперь обозначение y_n+1 = x_n. Тогда

.

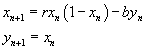Это и есть искомое двумерное отображение. Если использовать другое представление для квадратичной функции, то это отображение можно записать в виде

.

Такое отображение впервые предложил французский астрофизик Мишель Эно, и оно носит его имя. (Эно не использовал биологическую интерпретацию, а исходил из другой мотивации - искал простейшие двумерные квадратичные отображения со сложной динамикой.)

Интересно, что отображение Эно можно получить и для простой физической системы.

Пусть в воде плавает лодка массы m, на которой установлен двигатель, включающийся периодически с периодом T на очень короткое время (рис.1). Пусть за это время лодка получает импульс P. Будем считать, что сила сопротивления пропорциональна скорости с коэффициентом k.

Рис.1

В промежутке между моментами работы двигателя лодка движется свободно. По второму закону Ньютона

,

где F_C - сила сопротивления, a - ускорение лодки. По условию F_C = kV, где V - ее скорость.

Далее нам понадобится понятие производной. Как известно, и . Тогда

.

Это простое дифференциальное уравнение. Решим его. Сначала перепишем это уравнение так

Тогда

Интегрируя, находим

.

Константу интегрирования C легко определить из начального условия: V(0)=V₀, тогда

Теперь вспоминая, что , получим

или

Интегрируя это уравнение, находим

Константу интегрирования опять находим из начального условия x(0)=x₀:

.

Тогда окончательно

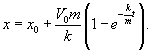
Пока мы просто решили задачу о движении лодки в случае, когда сила сопротивления пропорциональна скорости. Перейдем теперь к конструированию отображения.

Первый важный шаг при построении отображений - это выбор дискретные переменные. В нашем случае решение задачи "подсказывает", что удобно использовать значение координаты x_n и V_n непосредственно перед включением двигателя.

Двигатель работает очень короткое время и по условию сообщает лодке дополнительный импульс P. Тогда координата лодки сразу после действия двигателя не успевает измениться, а скорость получает добавку P/m:

Далее лодка движется свободно и можно воспользоваться нашим решением, используя найденные координату и скорость как начальные значения

Тогда через время T получим

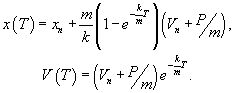
Но это значения координаты и скорости непосредственно перед (n+1)-ым импульсом! По нашему определению - x_n+1 и V_n+1. Тогда

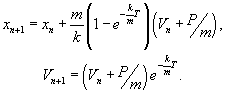
Итак, мы получили дискретное отображение для двух переменных x_n и V_n, как говорят, двумерное отображение.

Найденное нами отображение линейно и поэтому демонстрирует очень простую динамику. Представим себе, однако, что задача поставлена несколько иначе. Пусть на лодке укреплен магнит, а импульсы она получает от внешнего магнитного поля, включаемого на короткое время (рис.2).

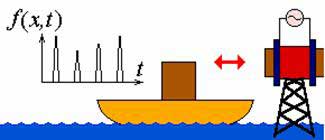
Рис.2

В этом случае магнитное поле будет разным в разных точках и поэтому P=P(x), где функция P(x) характеризует распределение этого поля.

Тогда получим

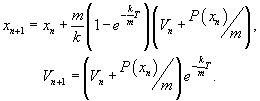
Или, что то же самое:

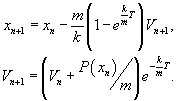
Из первого уравнения видно, что удобно ввести замену переменной

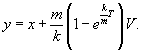
Действительно, тогда y_n+1=x_n. В свою очередь

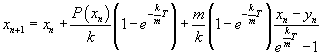
или

где и .

Мы получили искомое двумерное отображение

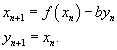
Ясно, что нужно как-то конкретизировать функцию f(x). Простейшее предположение состоит в том, что это квадратичная функция . Тогда

Мы пришли к отображению Эно.

Обсудим теперь кратко некоторые свойства этого отображения. Отображение Эно при b=0 превращается в логистическое отображение. Поэтому для него естественно ожидать аналогичное поведение.

Найдем, прежде всего, неподвижную точку:

Тогда Откуда

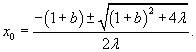
Неподвижных точек две, как и у логистического отображения. Они существуют при условии:

Найдем теперь 2-цикл:

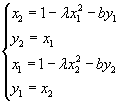
Подставляя второе уравнение в третье и четвертое в первое, получаем

,

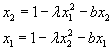или

.

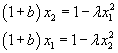Складывая и вычитая эти уравнения, получим

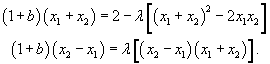
Если , то из второго уравнения следует, что

а тогда из первого -

.

По теореме Виета элементы 2-цикла ищем из квадратного уравнения

Откуда

Таким образом, 2-цикл возможен при условии:

При b=0 получаем - значение, при котором неподвижная точка теряет устойчивость и рождается 2-цикл. Естественно предположить, что аналогичная ситуация имеет место и в отображении Эно, хотя доказать это значительно сложнее. Мы этого делать не будем, а используем компьютерное моделирование.

На следующем рисунке показано бифуркационное дерево отображения Эно при b=0,3. Можно видеть, что оно не только демонстрирует рождение устойчивого 2-цикла из неподвижной точки, но и весь каскад бифуркаций удвоения периода, хаос и окна непериодичности в хаосе. Новым является то, что дерево иногда скачком "разбухает". Такое явление в нелинейной динамике назы вают кризисом.

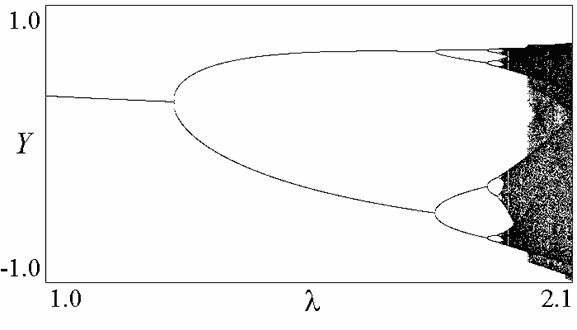
Рис.3

Надо сказать, что мы описали лишь простейшие свойства отображения Эно. На самом деле его динамика столь многообразна, что ему можно посвятить целую монографию. Более того, многие современные исследователи по-прежнему используют отображения Эно в своих работах.

Задачи

1. Нарисуйте на плоскости b, 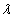область существования устойчивой неподвижной точки. Параметр -1<b<1.

2. Создайте программу, рисующую бифуркационное дерево для отображения Эно. Постройте его для случаев b=0,3, b=0,6, b=0,9. Что происходит с деревом при приближении b к единице?