Отображения на примере школьной задачи
Практически в любом сборнике олимпиадных задач по физике можно найти задачу о бесконечной цепочке резисторов. Она формулируется так: чему равно сопротивление изображенной на рис. 1 цепочки резисторов, которая состоит из одинаковых звеньев (рис.1)?
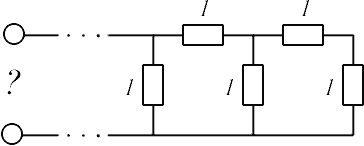
Рис.1
Сопротивления всех резисторов одинаковы, и мы будем полагать их равными единице. Традиционное решение этой задачи основано на соображении о том, что добавление еще одного звена к бесконечной системе не изменяет ее, т.е. данная схема эквивалентна показанной на рис. 2.
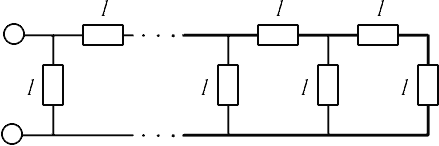
Рис.2
В результате приходим к схеме, показанной на рис.3.
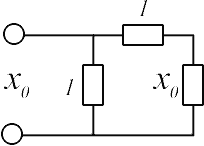
Рис.3
Здесь x0 – искомое сопротивление. Нетрудно получить, что
![]() , или
, или ![]() .
.
Тогда
![]() .
.
Откуда следует ответ к задаче:
![]()
Описанный метод в журнале “Квант” в статье, посвященной методам вычисления сопротивлений различных схем, назвали методом Иона Тихого – по имени известного героя Станислава Лема, сумевшего разместить постояльца в полностью заполненной гостинице с бесконечным числом номеров.
Такое решение, хотя и весьма изящно, но оставляет некоторое чувство неудовлетворения, поскольку остаются открытыми некоторые вопросы. В первую очередь: какое отношение к реальности имеет эта задача и это решение? Ведь реальная цепочка будет содержать конечное число звеньев. Можно сформулировать вопрос так: если мы можем измерять сопротивление с заданной точностью, то сколько звеньев должна содержать цепочка, чтобы считаться бесконечной? Кроме того, если вдуматься, то заранее не очевидно, что добавление новых звеньев в реальной конечной цепочке будет приближать результат измерения сопротивления к значению x0. Вдруг малые погрешности, которые вносят реальные резисторы, будут вносить нарастающий вклад, ведь цепочка бесконечная.
Оказывается, на все эти вопросы можно ответить, привлекая изящный математический аппарат дискретных отображений, являющийся частью современной теории динамических систем.
Итак, обратимся к нашей схеме, отсчитаем конечное число звеньев n и n+1 от правого конца (рис.4).
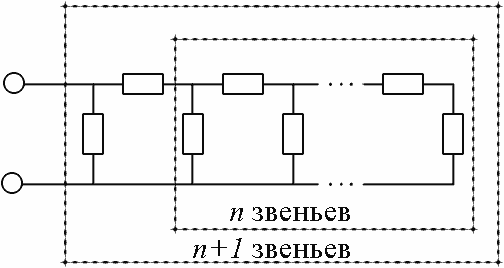
Рис.4.
Из рисунка хорошо видно, что схема эквивалентна такой:
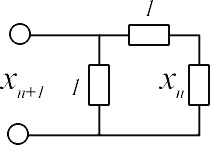
Рис.5
Отсюда легко получаем
![]()
Это и есть простейший пример дискретного отображения. В общем виде одномерное дискретное отображение задается соотношением
![]()
(В нашем случае ![]() ) Мы назвали отображение одномерным, поскольку в него входит одна
переменна – x.
) Мы назвали отображение одномерным, поскольку в него входит одна
переменна – x.
Дискретное отображение xn+1=f(xn) является, по-видимому, простейшим примером динамической системы. Смысл этого термина раскрывается просто: отображение xn+1=f(xn) по заданному начальному значению x1 позволяет определить все последующие значения переменной x2, x3 и т.д. Действительно:
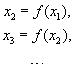
Свойства дискретных отображений удобно иллюстрировать на так называемой итерационной диаграмме. Для ее построения надо прежде всего изобразить график функции f(x). В нашем случае это перевернутая гипербола, смещенная влево на две единицы и на одну единицу вверх (рис.6). (Заметим, что поскольку сопротивления положительны, то смысл имеет лишь кусок графика в первой четверти.)
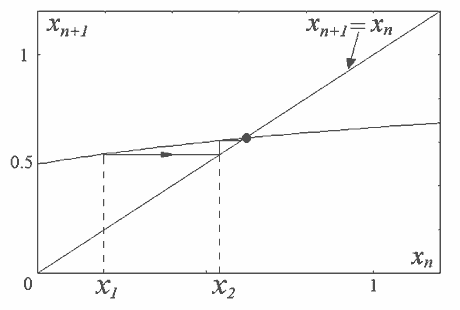
На графике изображается еще и биссектриса. Задавшись теперь начальным значением x1, можно найти x2=f(x1) по графику. Затем это значение переносится на биссектрису и процедура повторяется. Возникает своеобразная лесенка, иллюстрирующая ход итераций.
Как видно из графика, наше отображение имеет, как говорят, неподвижную точку, т.е. такую, для которой x0=f(x0). Она как раз соответствует решению задачи по методу Иона Тихого.
По рисунку получается, что последовательные итерации сходятся к неподвижной точке. Как это доказать более строго? Каков характер сходимости (быстрый, медленный)? На эти вопросы можно ответить в общей формулировке.
Для этого исследуем поведение системы в случае, когда значений переменной близки
к предельному значению x0. Положим поэтому ![]() и
и ![]() , где знаком "тильда" сверху обозначены малые добавки к x0.
Тогда из
, где знаком "тильда" сверху обозначены малые добавки к x0.
Тогда из ![]() имеем
имеем
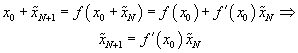
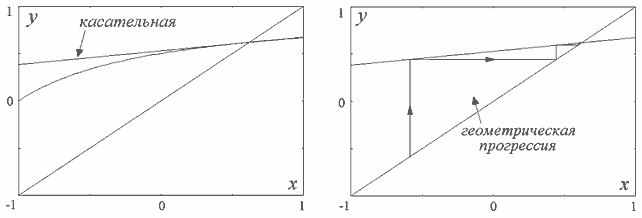
Таким образом, если имеется некоторая маленькая добавка к значению x0, то после первой итерации она умножается на постоянное число C= f '(x0), после второй – на C2, после третьей – на C3 и т.д. Это означает, что переменная x приближается к неподвижной точке по закону геометрической прогрессии с показателем C. Отметим, что наше рассмотрение на итерационной диаграмме соответствует тому, что мы аппроксимируем f(x) касательной (вспомните геометрический смысл производной!) в окрестности x0 Соответствующая итерационная диаграмма и дает геометрическую прогрессию (рис.7).
Теперь по свойству геометрической прогрессии автоматически получаем, что если
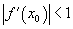 , то
итерации сходятся;
, то
итерации сходятся;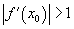 , то
итерации расходятся.
, то
итерации расходятся.
Это, как говорят, позволяет судить об устойчивости неподвижной точки.
В первом случае неподвижную точку называют устойчивой, а во втором – неустойчивой.
Сходящийся процесс мы уже изобразили на итерационной диаграмме, а расходящийся может выглядеть так (рис.8):
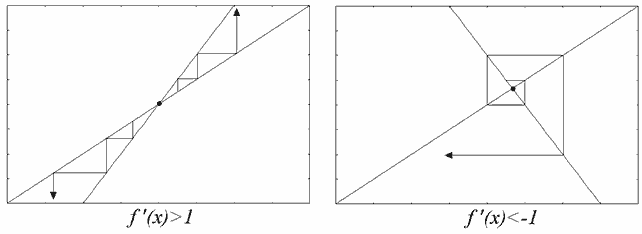
Рис.8.
Вернемся от отображения общего вида к нашему случаю. Тогда
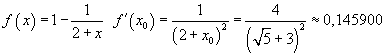 .
.
Итак, как мы видим C=0.145900. Это означает, что итерации сходятся, причем поскольку f '(x0) мало, значит, сходятся очень быстро. В этом убеждаемся, итерируя соотношение
![]()
Результат представлен в следующей таблице.
| Число звеньев в цепочке, N |
xN |
% |
| 1 |
x1=1 |
|
| 2 |
x2=2/3 |
7,86 |
| 3 |
x3=5/8 |
1,12 |
| 4 |
x4=13/21 |
0,16 |
| 5 |
x5=34/55 |
0,02 |
| … |
… |
… |
| |
x0= |
0 |
Мы убеждаемся, что увеличение числа звеньев действительно приводит в неподвижную точку. Из таблицы видно, что оказывается цепочку всего из трех звеньев можно считать бесконечной с точностью до 1%, а из пяти – уже с точностью всего 0,02 %!
Устойчивость неподвижной точки этого отображения снимает и еще один физический вопрос: о том, не «испортят» ли возможные дефекты в цепочке результат нашего решения. Продумайте сами, почему это так и изобразите соответствующие итерационные диаграммы.
Нам осталось сказать, что в силу большой важности величины f '(x0)
она носит специальное название – мультипликатор, и обозначается обычно
![]() .
.
Задачи
- Шарик падает с некоторой высоты на горизонтальную поверхность. При каждом
ударе о поверхность шарик теряет долю скорости
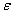 . Напишите отображение, задающие зависимость высоты (n+1)-го подскока
от n-го. Какую последовательность образуют высоты подскоков?
. Напишите отображение, задающие зависимость высоты (n+1)-го подскока
от n-го. Какую последовательность образуют высоты подскоков?
- Что будет, если в задаче о цепочке сопротивлений начальное (крайнее правое) сопротивление на рис.1 равно 100, а остальные – по-прежнему равны 1?
- Покажите, что отображение xn+1= (xn+a / xn)/2 можно использовать для вычисления квадратного корня из числа a (такой способ применяли еще в древнем Вавилоне). Найдите первые пять членов последовательности xn, порождаемой этим отображением при a=2. Величину x1 положите равной единице. Проиллюстрируйте решение задачи с помощью итерационной диаграммы. Покажите, что неподвижная точка этого отображения устойчива. Можно ли использовать отображение xn+1= a / xn? Почему?
- Найдите неподвижные точки и исследуйте их устойчивость для отображения xn+1 = axn-bxn3.
- Как будет выглядеть итерационная диаграмма для отображения, дающего арифметическую прогрессию?
- Напишите программу, которая строит итерационные диаграммы одномерного отображения для заданной функции f(x) и заданного начального значения x1.
- Изготовьте цепочку сопротивлений и проверьте в эксперименте данные таблицы из текста. При использованной Вами точности приборов и изготовления резисторов сколько элементов в цепочке будет достаточным?
Саратовская группа теоретической
нелинейной динамики