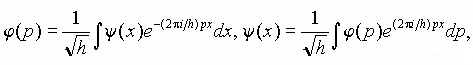
As known, for the one-dimensional quantum motion the wave function in position representation y(x) and in momentum representation j(p) are linked as the forward and backward Fourier transform:

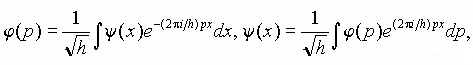
where h is the Planck constant. Let now the functions y(x) and j(p) have periods L_x and L_p, respectively. The periodicity of y(x) implies that its Fourier transform j(p) is a "comb" of d-functions, on the axis of wave numbers at points 2pn/L_x, that is with a step in momentum Dp=h/L_x. As the function j(p) is periodic too, its period L_p must contain an integer number of steps: L_p/Dp=N. Substituting here the expression for p, we obtain L_xL_p=hN, where N is an integer.

Hence, in the momentum representation the wave function is fully determined by N complex coefficients j_k, the factors at d-peaks.

Analogous consideration may be performed in the inverse order to conclude that the function y (x) is a "comb" of d-functions on the x-axis at points x=hm/L_p, that is with a step Dx=h/L_p and with an integer period. So, we again come to the relation L_xL_p=hN. In the position representation the wave function also is determined by N complex numbers y_m, m=0,1,...N-1.

Thus,

1) the Hilbert space of states for our system is the N-dimensional complex vector space.

2) Non-contradictory quantization is possible only under restriction on the parameters of the system expressed by relation L_xL_p=hN.

As known, one of the basic statements in the quantum mechanics is a requirement that at h®0 the correspondence with classic mechanics should take place. In the dynamics on torus, we cannot treat h as a continuous variable, but we can consider the passage to the limit on a discrete set of values allowed by the formula L_xL_p=hN. In this sense, the classic limit corresponds to N®¥.

Speaking on the position representation, we mean now simply an N-dimensional vector y_m, and in the momentum representation a vector j_k, respectively. It is easy to check that these two sets of numbers y_m and j_k are linked by the discrete Fourier transformation:

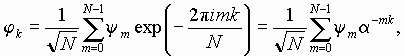
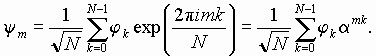
Here we use the notion a=exp(2pi/N), which will be used below. For operators of the forward and backward Fourier transformation we adopt the symbols F and F⁺. They are represented by matrices of size NxN, with elements F_mn=a^-mn/N^1/2, F⁺_mn=a^mn/N^1/2.

If the periods L_x and L_p are unit, then y(x) and j(p) are represented as "combs" of d-functions with one the same step 1/N; so the quantum constant must satisfy h=1/N.

In the commonly used Dirac notion, the column vector is called the ket-vector |a>, where a is a symbol marking the given state. A conjugate row vector is called bra-vector <b|, and their scalar product ("bracket") is <b|a>. In our case these are the N-component vectors:

|a>={a₀, a₁,...a_N-1}^T, <b|={b₀, b₁,...b_N-1}, and <b|a>=b*₀a₀+b*₁a₁+...+b*_N-1a_N-1.