Up to here we considered discrete-time models represented by iterative maps. Let us discuss a possibility of realization of SNA in systems governed by usually preferred by physicists differential equations. A key point is establishing a link between the differential equations and a description in terms of maps on a basis of the idea of the Poincare section for the class of systems with quasiperiodic driving.
Let us suppose for definiteness that whithout driving a continuous-time system had a two-dimensional phase space (x, y) and was governed by a set of two differential equations of the first order. In the case of two-frequency external driving the coefficients will be periodic functions of two phase variables Q и F, which vary linearly in time:
![]()
A frequency ratio w/W is supposed to be irrational. Let we have some values of the variables (x, y, Q) at the definite phase of the second component F. What will be these values after one period of this component T=2p/W? From the uniqueness theorem it follows that they are definite functions of the original values. After one more period they are obtained by a repetitive application of the same functions, and so on. Therefore, we get an iterative map,
![]()
Formally, we deal with a cross-section of the four-dimensional phase space (x, y,Q,F) by a hyper-plane F=const, and speak on a mapping of this hyper-plane into itself. (Note that in F the phase space has a periodic structure, so we may identify points with F coinciding up to an integer number of T.) In the context of our problem, this is precisely the Poincare map, called also the stroboscopic map.
Now we can forget about the original differential equations and concentrate on analysis of dynamics generated by the Poincare map. This change of a subject of a study is not an approximation; the analysis remains accurate. The price is a loss of information about dynamics in time intervals between subsequent cross-sections and about topological properties of the orbits. However, it is possible yet to examine relevant questions, say, which kind of attractor is realized, regular, chaotic, or SNA.
With rare exceptions, the functions F1 и F2 may be obtained only from numerical solution of the differential equations. However, in principle, it is clear that we have a problem of the same type as the discrete-time models, the iterative maps under quasiperiodic driving. We may add, that in systems with strong dissipation, the states observed in a course of the dynamical evolution in the cross-section at each fixed Q have a tendency to dispose along a curve in the plane (x, y). In this case, introducing instead of the pair of variables (x, y) a single coordinate along this curve we arrive to a reduced description in terms of one-dimensional quasiperiodically driven map.
A representative and widely studied class of nonlinear systems includes the forced dissipative nonlinear oscillators. As an example, in the following set of plots we present numerical results relating to a Duffing oscillator with parametric quasiperiodic excitation (Heagy and Ditto, J.Nonlinear Sci., 1, 1991, 423):
![]()
where w=2p,
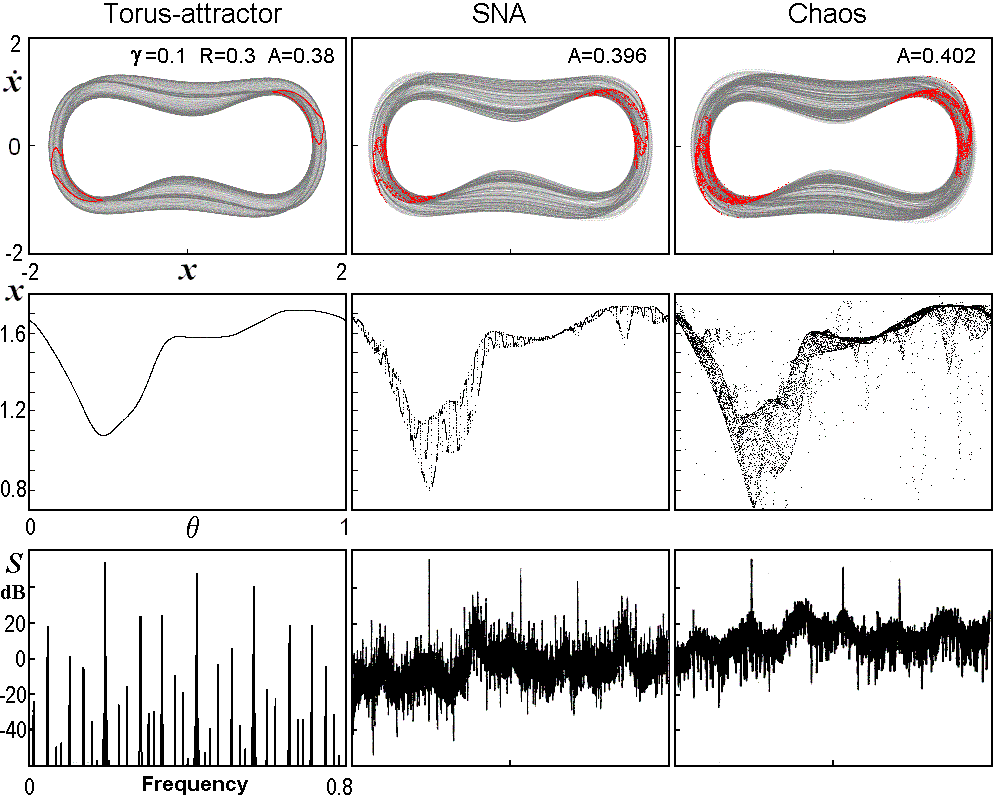
The first reported experimental observation of SNA relates to a mechanical oscillator consisting of a magneto-elastic ribbon with one fixed end, exiting by a quasiperiodically varying magnetic field (Ditto at al., Phys. Rev. Lett., 65, 1990, 533). The system is governed by a non-autonomous Duffing equation. The SNA regime was identified based on a view of the phase portraits, scaling behavior for spectral components associated with a singular-continuous spectrum, and on dimension characteristics: estimates of fractal and information dimensions for the Poincare section of the attractor wer found to be close to 2 and 1, respectively. Also, it was reported on observation of SNA in numerical computations in a quasiperiodic system of self-oscillator type, the van der Pol system (Kapitaniak et al., J.Phys. A: Math.Gen., 23, 1990, L383), in experiments with nonlinear oscillators constructed as electronic analog devices governed by certain differential equations (Zhou et al., Phys.Rev. A45, 1992, 5394; Yu et al., J. Korean Phys. Soc., 34, 1999, 130). Deside the phase portraits, spectra, and dimension estimates, the authors discussed compliment results related to Lyapunov exponents computed for the differential equations for which the studied electronic oscillators serve as analog models. In one of the mentioned works a transition to SNA via blowout bifurcation was realized and studied.
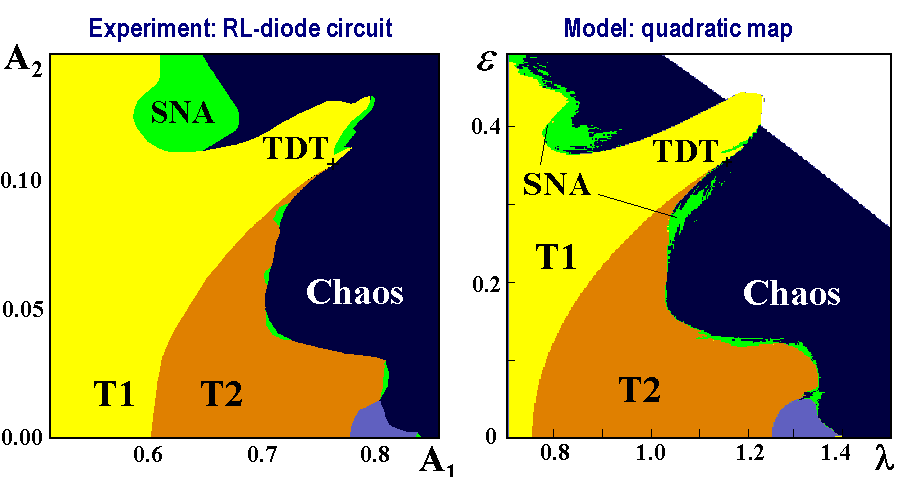
In a work of Bezruchko, Kuznetsov, and Seleznev (Phys. Rev. E62, 2000, 7287) an electronic oscillator was studied experimentally represented by a quasiperiodically excited RL-diode circuit. As known, in a case of one-frequency excitation it demonstrates the period-doubling transition to chaos, like the logistic map. Adding one more component of the excitation with a frequency, which is in irrational ratio with the first one (the golden mean), we get the same phenomena as in the quadratic map with quasiperiodic driving. Compare the following two charts of dynamical regimes, one obtained in the experiment with the electronic oscillator (plotted along the coordinate axes are the amplitudes of harmonic components of the excitation in Volts), and the second - in numerical computations for the quadratic map.
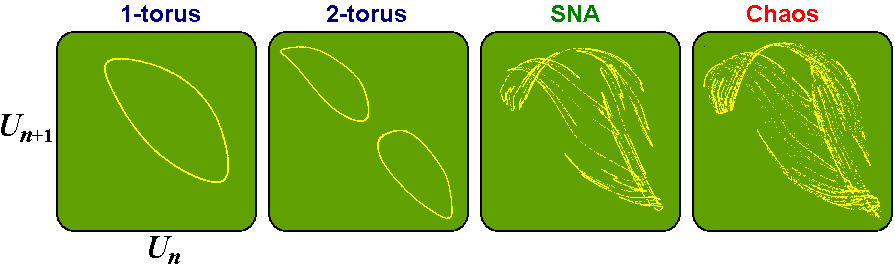
For identification of SNA, in the experiment the idea of Pikovsky and Feudel was used: in a case of frequency ratio given by a rational approximation of the golden mean (13/21), and at fixed rest parameters, it was possible to observe presence or absence of bifurcations in dependence on the phase relation between the components.
By the analog-digital transformer, output signal of the system, proportional to voltage on the resistor, could be introduced into a computer and processed. In particular, using data for output voltage with time step equal to one period of the basic frequency, we plotted them in coordinates (Un,Un+1) to obtain the iteration diagrams. In the following figure some examples of such diagrams are presented, corresponding to regimes of torus, doubled torus, SNA, and chaos.