main
this page only49. For cubic mapping 
find stability domain in a parameter plane a, b bounded by a line of the
tangential bifurcation and a line of period doubling bifurcation. Show, that the first
has a cusp point.
50. For cubic mapping from the previous problem stability domain of a 2-cycle have an appearance, typical for cycles of all periods for two-parameter mappings (cf. figure). K.Mira named such configurations "crossroad area". What lines of bifurcations are outlined in figure? Show the evolution of the twice iterated functions along several reference routes in the parameter plane and explain typicalness of such configurations. Find coordinates of a cusp point.
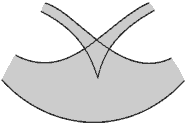
51. Taken previous mapping as an example, find the lines corresponding to mapping of a maximum onto a minimum and a minimum onto a maximum. Specify a point in the parameter plane, corresponding to a 2-cycle based simultaneously on two quadratic extrema. Show, that along the found lines the twice iterated mapping has an extremum of the fourth order.
52. For the fixed point of cubic mapping 
:
A. Find a curve of a multiplicator
( the tangential bifurcation) on a plane a, b. Show, that this curve has a cusp point and specify its coordinates. Figure all representative configurations of function
in a cusp point and its neighbourhood.
B. Find a curve of a multiplicator
and draw it on a plane a, b. Calculate a Schwarz derivative along this curve and specify, which segments of the curve correspond to a period doubling bifurcation, and which - to the hard transition (subcritical flip bifurcation). Specify a point of a codimension two on plane a, b in which the Schwarz derivative is vanishing (flip-bifurcation of a codimension two).
C. Find the equation the lines of the tangential bifurcation of a 2-cycle obey, and show, that they leave from the above found point with a zero Schwarz derivative and cross an a axis at points
D. Shade in figure stability domain of a 2-cycle. (the second typical configuration of two-parameter mappings - "spring-area" according to K.Mira's classification).
53. Draw the representative transformation of the twice iterated mapping from the previous problem in a neighbourhood of a point of a flip-bifurcation of a codimension two.
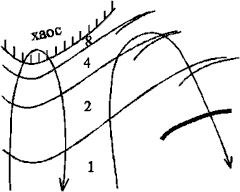
54. Draw qualitatively the bifurcation diagrams corresponding to the two routes on a dynamic regimes chart shown in figure.
55. Find a condition providing an existence of a cubic inflection point for
mapping 
.
What object accounts for realizing this condition in space of three parameters a,
b, c? Find a condition relevant for the mapping of an quadratic extremum
onto a cubic inflection point. What object accounts for realizing this condition in
space of three parameters a, b, c? The same for a situation when
the cubic inflection point is mapped onto a quadratic extremum.
56. Show, that provided that quadratic extreme is mapped onto a cubic inflection point, the twice iterated mapping has an extremum of the sixth order. Picture the relevant situation on the iterative diagram. What is the codimension?
57. Show, that provided that quadratic extreme is mapped onto the other quadratic extremum, and the latter in turn - onto the other one, then the threefold iterated mapping has an extremum of the eighth order. Picture the relevant situation on the iterative diagram. What is the codimension?
Generate a dynamic regimes chart for one of the listed below mappings - i.e. prepare a picture of parameter plane on which the gray color toning designates cycles of a particular period. What lines of codimension-one bifurcations can be found out on your map? What points of bifurcations of a codimension two? Specify situations such as "crossroad area" and "spring area". Create the additional program which builds iterative diagrams at points of a map chosen by you. With the help of this program carry out the following investigation:
а) choose a route traversing several lines of period doubling and observe a period doubling cascade on the iterative diagram;
в) find cycles with small periods, for example 3 or 5, on stability islands in the field of chaos;
в) choose a point near to a line of the tangential bifurcation (before its threshold) and observe the relevant evolution of imaging point;
г) observe chaotic regimes;
д) explore evolution of attractors in a neighbourhood of a cusp point;
е) explore evolution of attractors in a neighbourhood of a critical point of a line of period doubling bifurcation (a flip-bifurcation of a codimension two).
"Overlook" enlarged fragments of a map inside which it is possible to observe interesting dynamics.
Examples of dynamic systems for examination:
а) cubic mapping 
;
b) cubic mapping 
;
c) quartic mapping 
.
main
education
this page only
top
