main this page only

Problems and lessons for course
"Theory of catastrophes"

education
program

Problems for topic "Catastrophe of a codimension two - cusp "

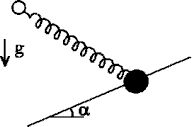
45. The blob of a mass m may slide without friction on a rod canted under an angle with respect to horizon. The blob is attached to a spring of a rigidity k which second end is fixed at a distance a apart from a rod at a point belonging to a vertical plane transiting through a rod (cf. figure). Length of a spring in an unstretched state is l. How is transformed at a modification of parameters the function describing the dependency of a potential energy on coordinate of a blob x, the coordinate being counted along a rod? Discover fold lines and a cusp point on a parameter plane , l/a.

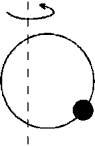
46. Small bead of mass m (figure) may slide without friction along a thin wire ring of radius R. A ring rotate with frequency around the vertical axis transiting through a plane of a ring at a distance a apart from its center. Trace the transformation of the functional dependency of the bead's potential energy on its coordinate in a rotated coordinate system. Discover fold lines and a cusp point on a plane of parameters a, .

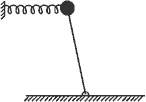
47. In figure the system representing a pendulum in the upper position of an equilibrium, attached to a spring is shown. Show, that if the spring is linear and its stiffness factor k is insignificant, the position of an equilibrium is unstable. Show, that if a spring is nonlinear then the cusp catastrophe is possible. Consider, that nonlinearity of a spring is featured by a relation , where k and c are the positive coefficients, and also an angle of deflection of a pendulum from a vertical it is small. Length of a rod l, a mass of a blob m.

48. Figure a surface obeying the equation of van der Waals gas in the space (pressure P, volume V, temperature T) and discuss its structure from the point of view of the theory of catastrophes. With the help of the computer or the calculator outline the fold lines and a cusp point in coordinates (P/P_c, T/T_c), where P_c and T_c are critical values of temperature and pressure known from thermodynamics. On the same graph draw a "semicubical" edge approximation.

49. In figure the volt-ampere characteristic of a semiconducting radio engineering device a tunnel diode is shown. Such diode is included in a circuit containing tunable electromotive force source E with interior resistance R.

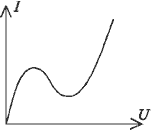
Find a cusp point and a fold lines on a parameter plane (E, R). Use cubic approximation of a volt-ampere characteristic , where a, b and c are the coefficients.

50. Parameters of the system demonstrating cusp catastrophe are slowly tuned so that the point on a parameter plane bypasses cusp 5 times (cf. fig). How many jumps (sudden transitions) happen in a system? For routes shown in the figure, outline (in a qualitative way) the dependency of the system state on the parameter counted along these routes.

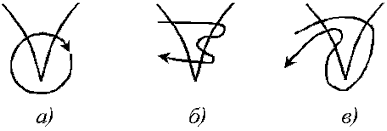
51. How the parabolic rocking chair will behave if to attach a magnet at a point of cusp?

52. What is the difference between the properties of a nonlinear oscillator in cases when the a potential energy dependency on coordinate has catastrophe of cusp or dual cusp?

53. Figure various possible projections of a torus onto a plane. Specify points of cusp which arise at such projection. Discuss a problem of a stability of cusps at small perturbations of a torus.

54. Show, that a trajectory of a point on a rim of the wheel rolling without a slippage, has edges with the distinctive "semicubical" singularity.

Computer lessons for topic "Oscillations of an oscillator with two-well potential "

Construct phase portraits of a conservative and dissipative oscillator with a potential, corresponding to a cusp catastrophe U(x)=x⁴/4+ax²/2+bx. Create the program showing the form of potential function and phase portraits at various points of a plane a, b. Beforehand superimpose on it lines of folds and a point of cusp. It is convenient to observe the evolution of pictures, if change of parameters (coordinate of the point chosen on the screen) is realized with the help of "mouse".

Computer lessons for topic "The two-dimensional pendulum in a field of three attractive bodies"

Consider a motion of a two-dimensional pendulum with attenuation, located at the centre of the equilateral triangle in which vertexes there are three attractive centres (magnets, gravitational masses etc.) Consider, that the potential corresponds to a gravitation low. Figure a pattern of level lines of such potential and its relief. Show, that in the vicinity of the centre it corresponds to a catastrophe of an elliptic umbilic. Show some of the reference trajectories of a pendulum. Discover basins of an attraction of equilibrium states of a pendulum.

main education this page only top