main
this page onlyA square frame made of conducting wire may rotate without friction around the axis ОО' (see Figure).
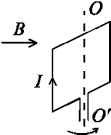
Current in the wire forming the frame equals I. The frame is placed in magnetic field B that is perpendicular to the axis of the frame. Prove that oscillations of the frame are governed by the equation of pendulum. Mass of the frame equals m.
Reduce
approximately the problem of motion of a particle of mass m in a potential relief
to the model of oscillator with cubic nonlinearity. Compute nonlinear
correction to the frequency in this approximation for oscillations of small
amplitude, and compare it with the exact analytical result obtained for the
original oscillator. Present respective table with data for different
amplitudes.
A ball of mass m having positive electrical charge q slides without friction along a non-conducting pin (see Figure).
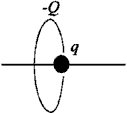
The pin is perpendicular to the plane of a non-moving ring of radius R and crosses this plane at the center of the ring. The ring has negative electrical charge -Q. Consider small oscillations of the system and approximate it by oscillator with cubic nonlinearity. Which features of the system are caught correctly by the model? Which are not? Estimate a relative shift of the frequency at a particular amplitude R/3.
Use model of oscillator with cubic nonlinearity to estimate an angular amplitude for pendulum necessary to reach 1% deflection of the oscillation period from the value predicted by the linear theory.
Use model
of oscillator with cubic nonlinearity to estimate ratio of amplitudes of the first and
the third harmonics in spectrum of pendulum oscillations for angular amplitudes
and 
.
Derive
analytical expression for nonlinear correction for frequency of small
oscillations of pendulum. (Hint: Use formula for Fourier expanding of sin(xsin
) with Bessel functions
as coefficients.) Prove that the correction agrees in the first order with the
result for the oscillator with cubic nonlinearity. Estimate period of
oscillations with angular amplitude 
. Compare this estimate with exact result and with the result
for the cubic nonlinear oscillator.
A pendulum
in the upper equilibrium position is attached to a nonlinear spring. The
nonlinear characteristic of the spring is given by relation
, where k and c
are positive constants. Angle
of deflection from vertical is small. Length of the rod of the pendulum is l, mass of
the ball is m. Which model of the universal nonlinear
oscillators you prefer to use at 
and at 
? Derive respective equations in the explicit form. Estimate
frequency correction and a value of a shift of center of oscillations.
A molecules oscillates in a potential of Lenard-Jones. Represent the system by a model of quadratic nonlinear oscillator. Using this model estimate an increase of distance between the molecules when amplitude of the oscillations equals a. Use the result to explain thermal expansion of solids.
Derive
relation for nonlinear correction to a frequency of oscillations in a system
governed by the equation 
Undertake the following study of the pendulum equation.
a) Compose an animation program to show motion of pendulum on the computer screen.
b) Plot an angular coordinate and velocity of the pendulum versus time. Observe small oscillations, moderate amplitude oscillations, motion close to separatrix. Using a distinct color, for moderate amplitude plot on the same picture a solution obtained from method of slow amplitudes. Compare the approximate and exact curves. Do the same for the motion near separatrix.
c) Plot a period of oscillations versus angular amplitude using either exact expression via the elliptic integral, or numerical simulation of the oscillations to determine periods. Compare these results with data obtained in approximation of weak nonlinearity.
d) Plot a Fourier spectrum for velocity of the pendulum and observe its evolution with increase of the amplitude from small oscillations up to motions near separatrix. Compare the numerical result with respective analytical solution.
e) Plot phase portrait of conservative and dissipative pendulum on the computer screen, observe its transformation with growth of the dissipation parameter.
main
education
this page only
top