главная наука только эта страница

Постановка задачи

Нестационарные процессы в системе электронный пучок - электромагнитная волна вблизи границы полосы пропускания описываются следующими уравнениями с граничными и начальными условиями:

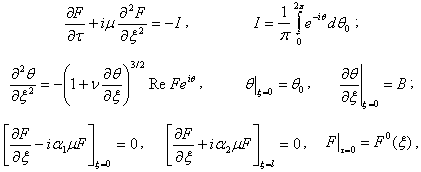	(1)
	(2)
	(3)

где и - безразмерные время и координата, F - комплексная амплитуда высокочастотного поля, 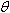- фазовая координата электронов, l - безразмерная длина пространства взаимодействия, B - параметр рассинхронизма пучка с колебаниями поля на границе полосы, - параметры граничных условий, - релятивистский параметр, выбор: соответствует высокочастотной границе, - низкочастотной. Функция характеризует начальное распределение поля по длине системы. Соотношение (1) - это уравнение возбуждения, (2) - уравнение движения, (3) - граничные условия.

При исследовании динамики данной системы обычно используют следующие безразмерные комбинации физических величин:
Параметр l регулируется изменением рабочего тока электронного пучка. Он пропорционален корню четвертой степени из величины тока.
Комбинация Bl характеризует относительный угол пролета электронного пучка и волны критической частоты. Практически параметр Bl управляется ускоряющим напряжением.
Вместо времени используется комбинация , нормировка которой не зависит от тока и напряжения.
Параметр , входящий в уравнение движения (2), из-за предполагаемой малости может быть значительным только в ультрарелятивистском случае. Поэтому значения соответствуют нерелятивистскому случаю, а - релятивистскому. Вместо параметра используют комбинацию .
Условия на концах пространства взаимодействия, определяемые устройствами ввода и вывода энергии, характеризуются комбинациями и . Для определенности будем полагать, что в некоторой точке полосы пропускания система полностью согласована. При этом параметры и равны друг другу. Реалистичные значения составляют ~ 5 - 50.
Чтобы определить амплитуды сигналов, поступающих из системы во входной и выходной волноводы, используют энергетические соображения. Вводят безразмерные амплитуды сигналов как корень квадратный из безразмерного потока мощности в сечениях и :

(4)

Для численного решения данной задачи используют разностную схему второго порядка точности как по временному шагу, так и по временному. Уравнение возбуждения (1) аппроксимируют следующим выражением:

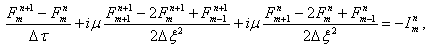(5)

где верхние индексы у величин , означают номер временного, а нижние - пространственного шага: .
Граничные условия записываются в следующем виде:

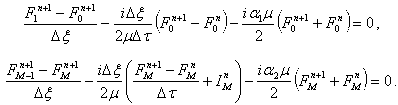(6)

Если известны величины , отвечающие n-му временному слою, то можно решить уравнения движения электронов в этом поле (2) и найти значения стандартным методом крупных частиц. Затем, с помощью метода прогонки находят предварительные, подлежащие уточнению, величины (n+1 временной шаг). С помощью усреднения значений поля на n-ом и n+1 шаге находят значения и по ним, решая уравнение движения, получают . По значениям поля на n-ом временном шаге и значениям тока на n+1/2 шаге находят уточненные величины . Далее процедуру повторяют.

главная наука содержание только эта страница в начало