Саратовская группа

теоретической нелинейной динамики

Вынужденная синхронизация двух связанных осцилляторов

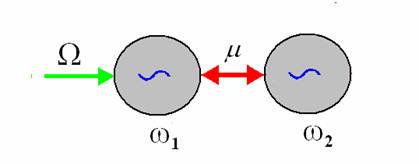
Система двух возбуждаемых внешним гармоническим сигналом диссипативно связанных осцилляторов Ван-дер-Поля описывается уравнениями

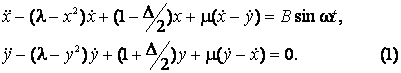
Здесь – параметр возбуждения автономных осцилляторов, – их частотная расстройка, – коэффициент диссипативной связи, B – амплитуда воздействия, – его частота. Центральная частота осцилляторов принята за единицу, так что представляет собой отстройку частоты сигнала от центральной.

Фазовое приближение

В рамках традиционных предположений о малой степени возбуждения осцилляторов, величине связи и т.д. система (1) может быть приближенно приведена к фазовым уравнениям:

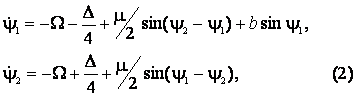
Здесь и – фазы первого и второго осцилляторов относительно внешнего сигнала, – параметр амплитуды воздействия.

Фазовые портреты и простейшие режимы системы

Динамика системы (2) протекает на плоскости фаз осцилляторов . В силу периодичности фаз можно считать, что движение происходит в пределах области . Примеры фазовых портретов системы (2), иллюстрирующие основные типы режимов, показаны на рисунке. Аттрактором системы может выступать состояние равновесия или притягивающая инвариантная кривая, которые выделены на рисунках красным цветом.

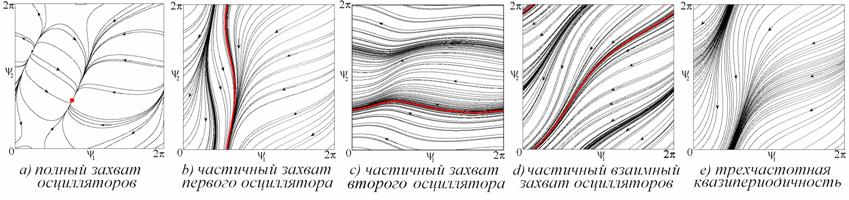
Охарактеризуем кратко представленные примеры.

a) Полный захват осцилляторов внешней силой. Фазы обоих осцилляторов и постоянны. Аттрактором на плоскости фаз является устойчивое состояние равновесия.

b) Частичный захват первого осциллятора внешней силой. Фаза первого осциллятора осциллирует около равновесного значения, фаза второго неограниченно нарастает. Аттрактором является инвариантная кривая.

c) Частичный захват второго осциллятора внешней силой. Фаза второго осциллятора осциллирует около равновесного значения, фаза первого неограниченно нарастает. Аттрактором является инвариантная кривая.

d) Частичный взаимный захват осцилляторов. Относительная фаза осцилляторов осциллирует около равновесного значения, фазы обоих осцилляторов относительно внешнего сигнала нарастают. Аттрактором является инвариантная кривая.

e) Трехчастотная квазипериодичность. Поток фазовых траекторий на фазовой плоскости.

Режим (a) отвечает периодическим колебаниям системы. Режимы (b,c,d) отвечают двухчастотной квазипериодичности. Режим (e) отвечает трехчастотной квазипериодичности. В системе, однако, возможны и другие типы двухчастотных режимов, которые обсуждаются ниже.

Динамика фаз на торе

Свойство 2π-периодичности фаз позволяет отождествить верхнюю и нижнюю границы области , а также левую и правую ее границы. В результате такой процедуры фазовое пространство трансформируется к тору, так что динамика фаз происходит на его поверхности.

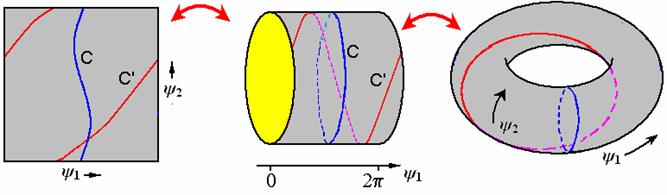
При этом аттракторы в виде инвариантных кривых превращаются в замкнутые орбиты на поверхности «тора фаз». Так кривая С, отвечающая частичному захвату первого осциллятора, трансформируется в замкнутую кривую, обходящую тор только по меридиану. Кривая С¹, отвечающая частичному захвату относительной фазы осцилляторов, делает по одному обороту по меридиану и по параллели.

Классификация режимов

Представление эволюции фаз осцилляторов в виде траекторий на торе позволяет дать простую классификацию квазипериодических режимов. Для этого каждой инвариантной кривой, лежащей на поверхности тора, можно приписать число вращения w=p/q, где p – число оборотов по поверхности тора по параллели, а q - по меридиану. Если вернуться к представлению в виде «фазового квадрата», то число вращения w определяется количеством p существенных пересечений инвариантной кривой с вертикальной и q – горизонтальной сторонами этого квадрата.

Представленные выше основные типы двухчастотных режимов, характеризуются следующими числами вращения: b) w=0/1, c) w=1/0, d) w=1/1. Трехчастотному квазипериодическому режиму (e) будет соответствовать «фазовый» эргодический тор, так что число вращения w иррационально. Существуют более сложные разновидности двухчастотных режимов. Например, на рисунке показаны фазовый портрет и инвариантная кривая на торе, которым отвечает число вращения w=1/2.

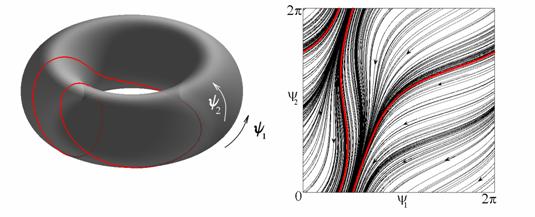
В терминах исходной системы (1) можно сказать, что в этом случае наблюдается резонансный двухчастотный тор, лежащий на поверхности трехмерного тора.

От языка Арнольда – к картине синхронизации квазипериодичности

Традиционным для неавтономных систем является описание типов режимов на плоскости параметров частота – амплитуда воздействия. В ситуации возбуждения простой автоколебательной системы геометрическим образом синхронных режимов является язык Арнольда, погруженный в область двухчастотной квазипериодичности.

В задаче о синхронизации квазипериодических колебаний картина трансформируется и усложняется. Для ее визуализации оказывается удобным построить карту ляпуновских показателей. С этой целью вычисляются оба ляпуновских показателя системы (2) в каждой точке плоскости параметров Затем эта плоскость окрашивается в соответствии с величинами показателей в разные цвета, чтобы визуализировать следующие режимы:

, периодический режим (точный захват фаз);

, двухчастотная квазипериодичность;

, трехчастотная квазипериодичность.

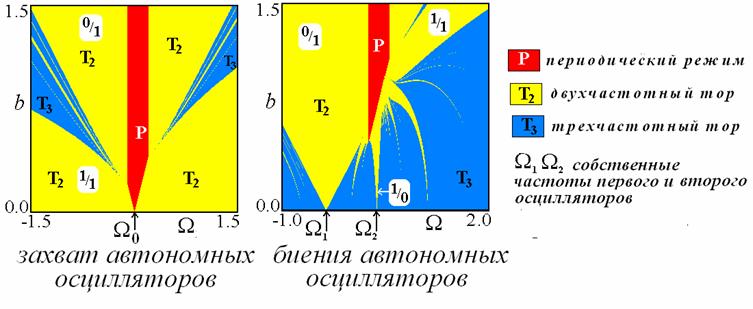
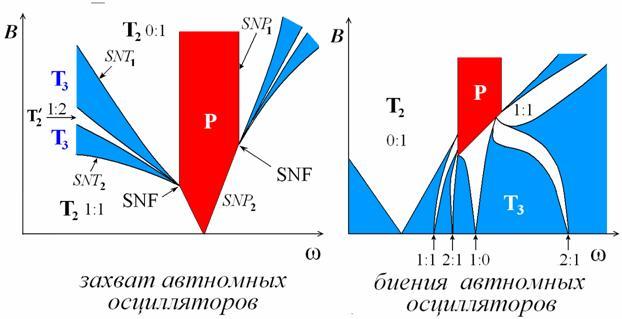
В результате визуализируются две «эталонные» картины. Первая отвечает режиму захвата автономных осцилляторов , а вторая – режиму биений автономных осцилляторов . На представленных картах обозначены также числа вращений простейших режимов.

Особенности синхронизации режима захвата. В этом случае область полной синхронизации имеет острие, основание которого отвечает частоте захвата автономных осцилляторов . При малых амплитудах воздействия наблюдается режим захвата относительной фазы осцилляторов w=1/1. С ростом амплитуды возникает трехчастотная квазипериодичность, чередующаяся с резонансными двухчастотными режимами, а при большой амплитуде сигнала наблюдается захват внешней силой первого осциллятора w=0/1.

Особенности синхронизации режима биений. В этом случае область полной синхронизации имеет порог по величине амплитуды воздействия. Ее продолжением в область малых амплитуд является язык, отвечающий захвату внешней силой второго осциллятора w=1/0. Наблюдается система языков резонансных двухчастотных режимов, имеющих основания на оси частот, и погруженных в область трехчастотной квазипериодичности.

Бифуркационные механизмы синхронизации двухчастотных колебаний

Рассмотрим бифуркационные механизмы разрушения (возникновения) синхронизации двухчастотных колебаний. За режим полной синхронизации отвечает устойчивое состояние равновесия фазовых уравнений (2). Полагая , легко получить, что

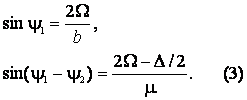
Соответственно, решения уравнений (3) при вариации параметров появляются парами. Таким образом, в системе возможно сосуществование четырех положений равновесия, которые на фазовой плоскости располагаются в вершинах параллелограмма. Это устойчивый и неустойчивый узел и два седла. Они имеют общий гетероклинический контур, как схематически показано на рисунке.

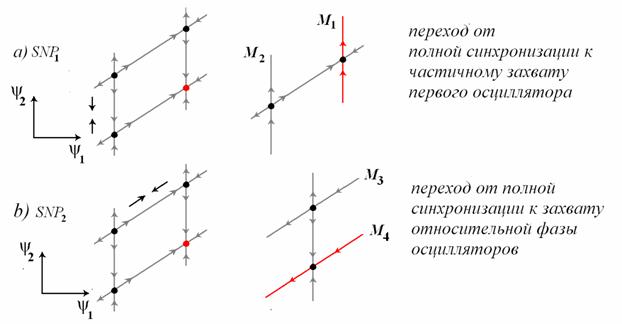
Обратимся к плоскости параметров частота – амплитуда воздействия в случае захвата автономных осцилляторов. В области P имеют место четыре равновесия. При выходе из этой области через границу они сближаются и одновременно попарно сливаются в результате специфической седло-узловой бифуркации, случай (а). В результате из многообразий состояний равновесия возникают устойчивая и неустойчивая инвариантные кривые, и возникает режим частичного захвата первого осциллятора внешней силой w=0/1.

При выходе через границу неподвижные точки сближаются и одновременно сливаются по другому сценарию (b), так что из их многообразий возникает устойчивая инвариантная кривая, отвечающая режиму частичного захвата относительных фаз осцилляторов w=1/1.

При выходе из двухчастотной области через линию происходит седло-узловая бифуркация инвариантных кривых с числом вращения w=0/1 в результате которой устойчивая и неустойчивая инвариантные кривые сливаются и исчезают. При этом возникает поток фазовых траекторий, отвечающий трехчастотной квазипериодичности. Аналогичная бифуркация, но для инвариантных кривых с числом вращения w=1/1 имеет место на линии .

На плоскости параметров имеют место характерные точки коразмерности два . Для них все четыре состояния равновесия системы на фазовой плоскости стягиваются в одну точку. Точки SNF играют важную роль в картине режимов и характерны для задач синхронизации квазипериодических колебаний. На плоскости параметров в такой точке сходятся области полной синхронизации, захвата первого осциллятора, захвата относительной фазы осцилляторов и трехчастотных колебаний. Последняя имеет вид языка с вершиной в точке . В свою очередь, область трехчастотной квазипериодичности пронизана системой языков резонансных двухчастотных режимов с числами вращения w=p/q. Самый широкий из них отвечает w=1/2. Благодаря характерной структуре языков двухчастотных режимов Baesens et al. называют аналогичные точки saddle node fan – «седло-узловой веер». Отметим, что границы всех языков двухчастотных режимов с вершинами в точке SNF образованы линиями седло-узловых бифуркаций соответствующих инвариантных кривых.

C. Baesens, J. Guckenheimer, S. Kim and R.S. MacKay. Physica D49, 1991, 3, p.87.

Карты торов

Двухчастотные режимы классифицируются с помощью чисел вращения Этот факт можно использовать для простого и эффективного метода анализа плоскости параметров системы. С этой целью в каждой точке плоскости параметров численно определяется число вращения w, а затем плоскость окрашивается в разные цвета в соответствии с величиной w. Ниже приведены примеры таких карт торов, демонстрирующих увеличенные фрагменты плоскости

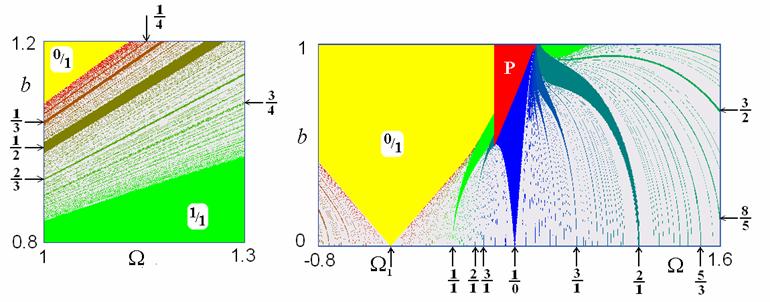
Первый рисунок иллюстрирует множество резонансных режимов разного типа внутри области трехчастотной квазипериодичности в случае захвата автономных осцилляторов. Второй позволяет более детально выявить картину двухчастотных режимов в случае биений.

Возбуждаемые связанные осцилляторы

Обратимся теперь к анализу исходной системы (1). Управляющий параметр выберем достаточно большим: , так что фазовое приближение, вообще говоря, не применимо.

Фазовые портреты и динамика фазы

Фазовое пространство системы (1) имеет размерность пять. Поэтому фазовые портреты можно представить в виде проекций на фазовые плоскости осцилляторов и . Поскольку система (1) является неавтономной, то информативными иллюстрациями являются так же стробоскопические сечения в этих проекциях, построенные через период внешнего воздействия. На приведенных ниже рисунках в первых двух колонках черным цветом показаны фазовые траектории первого и второго осцилляторов, а красным – соответствующие стробоскопические сечения.

Для исходной системы (1) анализ фазовой динамики можно провести только численным образом. С этой целью на плоскостях и введем фазу первого и второго осцилляторов и , как углы, под которыми изображающая точка видна из начала координат. Аналогичным образом можно ввести и фазы для стробоскопических сечений. Соответствующие иллюстрации даны в третьей колонке.

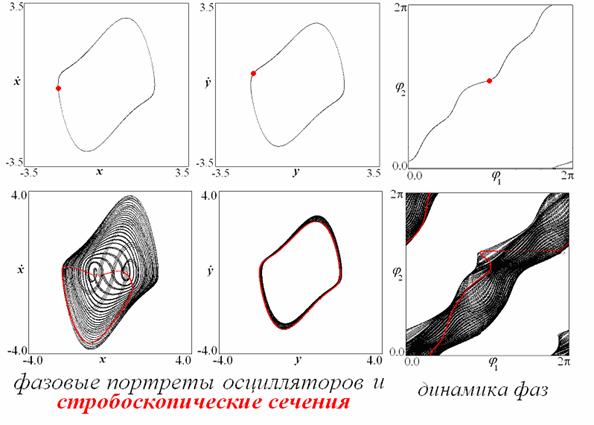
Первый из представленных примеров иллюстрирует режим полной синхронизации осцилляторов внешней силой. В этом случае фазовые портреты обоих осцилляторов представляют собой предельные циклы, близкие по форме к портретам изолированного осциллятора. В стробоскопическом сечении наблюдается неподвижная точка. Как видно из третьей колонки, фазы осцилляторов примерно близки друг к другу, а фазы в стробоскопическом сечении постоянны во времени.

Второй пример относится к режиму двухчастотной квазипериодичности. Тип режима определяем по числу пересечений инвариантной кривой в стробоскопическом сечении на плоскости фаз с вертикальной и горизонтальной границами области: w=1/1. Таким образом, наблюдается взаимный захват фаз осцилляторов. При этом, однако, внешняя сила велика, так что фазовый портрет первого осциллятора в левой колонке очень сильно возмущен внешним сигналом.

Отметим, что первый из рассмотренных примеров отвечает режиму, который возможен и в фазовых уравнениях, а второй уже не описывается в рамках фазового приближения.

Двухчастотные и трехчастотные торы и Фурье-спектры

Представим некоторые иллюстрации, характеризующие торы разных типов системы (1). Для этого используем проекции фазовых портретов в стробоскопическом сечении на плоскость скоростей обоих осцилляторов (x,y) – своего рода фигуры Лиссажу. Кроме того, представим соответствующие спектры Фурье первого осциллятора.

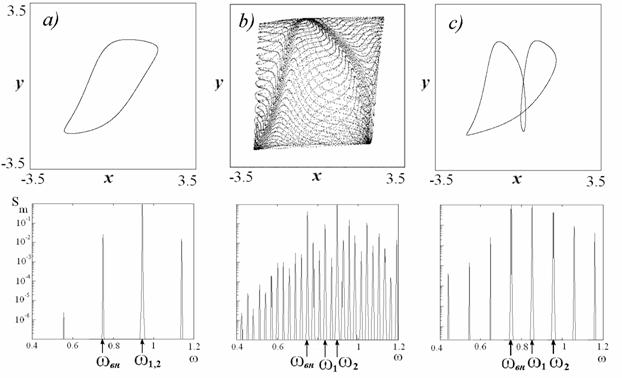
Случай (a) отвечает двухчастотному тору, когда осцилляторы взаимно захвачены w=1/1. Соответственно, фигура Лиссажу имеет по одной точке поворота по вертикали и горизонтали. В спектре колебаний доминирует пик на частоте , связанной с взаимным захватом осцилляторов и отмеченной стрелочкой. Частота воздействия отмечена другой стрелочкой. Остальные пики представляют собой комбинационные составляющие.

Случай (b) отвечают трехчастотному тору. Фигура Лиссажу для такого режима оказывается незамкнутой. На рисунке хорошо видны многочисленные точки поворота, как по вертикальной, так и по горизонтальной оси. Вместо в спектре появляется две основные несоизмеримые частоты и а также многочисленные комбинационные составляющие.

Случай (c) относится к резонансному двухчастотному тору, который возникает на поверхности трехчастотного. На фигуре Лиссажу в этом случае имеются две точки поворота по вертикали и одна по горизонтали, что соответствует числу вращения w=1/2. Пик на частоте располагается точно посередине между частотой воздействия и частотой :

что соответствует числу вращения w=1/2. При этом при движении по плоскости параметров в пределах данного языка частоты и меняются, но соотношение (4) сохраняется, что и отвечает резонансному типу такого тора.

Плоскость параметров возбуждаемых связанных осцилляторов Ван-дер-Поля

Плоскости параметров частота – амплитуда воздействия системы (1) в виде карт ляпуновских показателей для случаев захвата и биений автономных осцилляторов показаны на следующем рисунке.

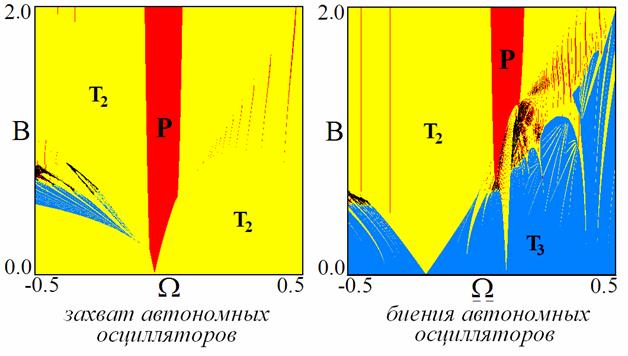
Можно отметить, что некоторые черты, выявленные в рамках фазового приближения, сохраняются и в случае больших управляющих параметров, однако, возникают и определенные отличия. Так для случая захвата автономных осцилляторов характерная для низкочастотной точки saddle node fan картина областей сохраняется, а для высокочастотной – разрушается. При этом на смену трехчастотной области приходят двухчастотные режимы со встроенной системой очень узких языков полной синхронизации высоких периодов: 3, 7, 12 и т.д. В режиме биений наблюдается новые дополнительные «веерообразные» системы узких языков двухчастотных торов. В обоих случаях наблюдается появление отмеченных на картах черным цветом незначительных областей хаоса с положительным ляпуновским показателем.

Механизмы синхронизации и ее разрушения

Обсудим возможные сценарии изменения колебательных режимов в соответствии с представленными картами. Иллюстрации удобно проводить в стробоскопическом сечении. Обратимся к случаю захвата автономных осцилляторов.

Первая серия рисунков иллюстрирует эволюцию стробоскопических сечений на плоскостях координат и фаз осцилляторов в низкочастотной области, если отстройка частоты сигнала невелика. В этом случае при малой амплитуде воздействия наблюдается взаимный захват осцилляторов (a). При увеличении амплитуды возникают режимы трехчастотной квазипериодичности (b), чередующиеся с резонансными двухчастотными режимами разного порядка (c), (d). Наиболее широкое «окно» отвечает резонансному тору с числом вращения w=1/2 (c). С ростом амплитуды можно наблюдать окна резонансных торов с числами вращения , например w=1/6 на рисунке (d) . При этом как на фазовом портрете первого осциллятора, так и на фазовой диаграмме появляется область «сгущения» траекторий, отмеченная на рисунке красной стрелочкой. При некотором пороговом значении амплитуды воздействия из этого сгущения возникает инвариантная кривая (е). Она отвечает режиму захвата первого осциллятора внешней силой w=0/1, что хорошо видно на плоскости фаз осцилляторов. Заметим, что непосредственно у порога такого перехода колебания первого осциллятора все еще происходят вблизи орбиты автономной системы. Таким образом, внешнее воздействие возмущает в основном фазу колебаний, так что в этом случае наблюдается сценарий, качественно аналогичный фазовому приближению. Соответственно, в случае (е) имеет место и неустойчивая инвариантная кривая. Ее столкновение с устойчивой инвариантной кривой и приводит к возникновению режимов типа (d).

Перейдем теперь к высокочастотной области. В этом случае с ростом амплитуды воздействия трехчастотные режимы не возникают. Тем не менее, наблюдается переход от режима захвата относительной фазы к захвату внешней силой первого осциллятора. Этот переход осуществляется в результате другого механизма. С ростом амплитуды воздействия инвариантная кривая первого осциллятора уменьшается в размере (переход от (a) к (b)). Затем наступает момент, когда она перестает охватывать начало координат (b). На плоскости фаз при этом происходит «перезамыкание» ветвей притягивающей инвариантной кривой, с переходом к виду, характерному для захвата первого осциллятора (c). Таким образом, захват первого осциллятора происходит через подавление автоколебаний за счет большой амплитуды внешней силы.

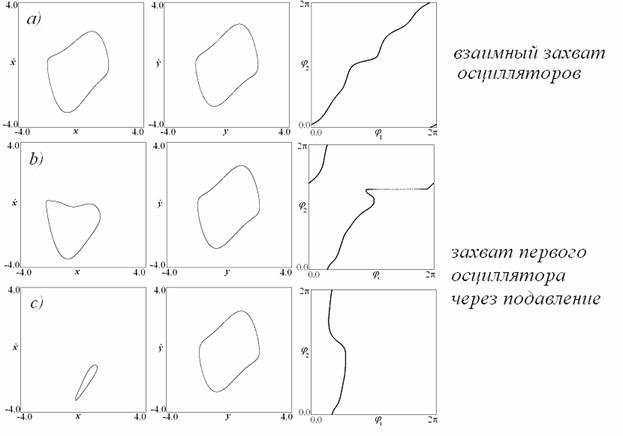
Следующие рисунки иллюстрируют эволюцию фазового портрета первого осциллятора, отвечающую этому механизму.

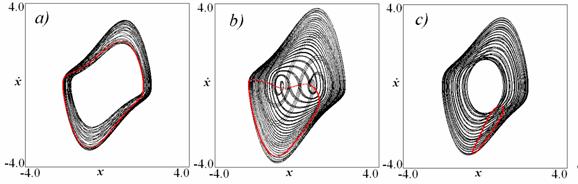
Сначала амплитуда колебаний возмущена не очень сильно (а). С ростом амплитуды воздействия возмущение орбиты осциллятора возрастает и становится настолько сильным, что изображающая точка начинает посещать начало координат. Инвариантная кривая в стробоскопическом сечении проходит через начала координат (b). С дальнейшим ростом внешней силы траектории снова уходят из окрестности начала координат, но теперь инвариантная кривая не охватывает начала координат (c). Возникает ситуация, когда внешняя сила существенно подавляет собственные автоколебания, возмущая не только их фазу, но и амплитуду.

Отметим, что аналогичный механизм реализуется и в одиночном осцилляторе, возбуждаемом внешней силой, однако, в очень узком диапазоне изменения параметров. (См. п.7.2.2 из Пиковский, Розенблюм, Куртс и соответствующее обсуждение.) В случае двух осцилляторов такие режимы занимают значительную часть плоскости параметров. Причина состоит в наличии второго осциллятора – он своими колебаниями разрушает точный захват первого осциллятора внешней силой.

Пиковский А., Розенблюм М., Куртс Ю. Синхронизация. Фундаментальное нелинейное явление. М.: Техносфера, 2003. 494 с.

Литература

1. Кузнецов А.П., Сатаев И.Р., Тюрюкина Л.В. Синхронизация квазипериодических колебаний связанных фазовых осцилляторов. Письма в ЖТФ. Т. 36, 2010, вып. 10, с.73-80.

2. Кузнецов А.П., Сатаев И.Р., Тюрюкина Л.В. Фазовая динамика возбуждаемых квазипериодических автоколебательных осцилляторов. Изв. Вузов. Прикладная нелинейная динамика. 2010. Т. 18, №4, 17-32.

3. Anishchenko V., Astakhov S., Vadivasova T. Europhysics Letters, 2009, v.86, p. 30003.

4. Анищенко В.С., В.В. Астахов, Вадивасова Т.Е, Феоктистов А.В. Нелинейная динамика, 2009. Т.5, N 2, с.237-252.

5. Кузнецов А.П., Сатаев И.Р., Тюрюкина Л.В. Вынужденная синхронизация двух связанных автоколебательных осцилляторов Ван дер Поля. Нелинейная динамика. Т. 7,  2011, №3, 411-425.

Синхронизация многочастотных и квазипериодических колебаний