Универсальное двумерное отображение с различными бифуркационными сценариями

атлас
след. - осциллятор Уеды
пред. - отображение Заславского

Модельное отображение

предложено А.П. Кузнецовым и С.П. Кузнецовым как пример, включающий все основные варианты потери устойчивости предельного цикла и соответствующие сценарии перехода к хаосу. Отображение содержит три параметра, S, J и e. S и J представляют собой не что иное как след и детерминант матрицы линеаризации отображения в неподвижной точке x=y=0. Эту точку можно мыслить как место пересечения секущей поверхности замкнутой траекторией - предельного цикла потоковой системы, для которой данное отображение служит отображением последования Пуанкаре. Параметр e с точки зрения качественных особенностей существенного значения не имеет и будет далее считаться фиксированной константой, e=0.35.

Имеется три типичных ситуации потери устойчивости предельного цикла:

один из мультипликаторов m становится равен – 1, тогда как второй по модулю меньше единицы (бифуркация удвоения периода);

один из мультипликаторов m становится равен 1, тогда как второй по модулю меньше единицы (седло-узловая бифуркация, которая может вести, в частности, к перемежаемости);

два комплексно-сопряженных мультипликатора становятся по модулю равны единице: |m|=1, т.е. лежат на единичной окружности (бифуркация Неймарка-Сакера, ведущая к рождению квазипериодического движения или, при резонансном соотношении частот - к рождению нового предельного цикла).

При линеаризации вблизи неподвижной точки в начале координат отображение принимает вид

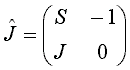
(Фактически наше приведенное выше модельное отображение и было сконструировано из этого соотношения путем добавления нелинейных квадратичных членов.) Мультипликаторы неподвижной точки получаются как собственные значения матрицы Якоби

из квадратного уравнения

Указанные выше бифуркационные условия отвечают трем сторонам треугольника, представляющего область устойчивости неподвижной точки на плоскости (S, J):

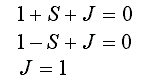
На рисунке слева показан общий вид карты режимов отображения на плоскости параметров (S, J), а справа в увеличенном виде фрагмент этой карты.

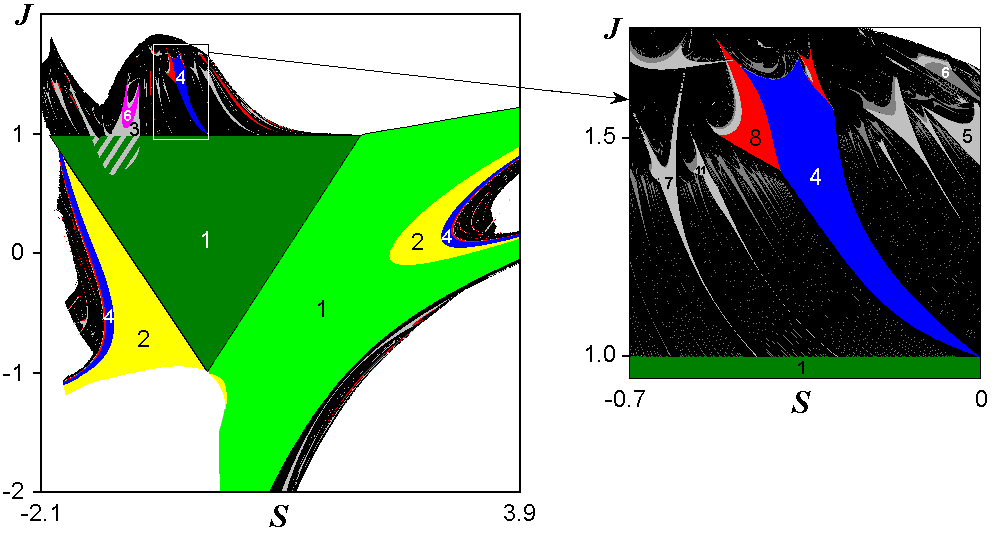
Области периодической динамики показаны цветом, и периоды обозначены цифрами. Черные области отвечают непериодическим режимам, включая квазипериодическое поведение и хаос. На диаграмме можно видеть зеленый (период 1) треугольник устойчивости, при переходе через левую строрну которого реализуется бифуркация удвоения периода с последующими бифуркациями и переходом к хаосу по Фейгенбауму. Правая сторона треугольника отвечает жесткому переходу, связанному с седло-узловой бифуркацией, а верхняя с переходом к квазипериодическому поведению через бифуркацию Неймарка-Сакера. Внутри области квазипериодичности можно видеть языки синхронизации, отвечающие рациональному соотношению частот возникших составляющих движения. Вершинам треугольника соответствуют бифуркационным ситуациям коразмерности два, когда мультиикаторы обращаются в (+1,+1), (+1,-1), (-1,-1).

Увеличенный фрагмент карты показывает детали устройства языка синхронизации 1:4, который опирается острием на линию бифуркации. Обратите внимание на отличие его структуры от случая стандартного синус-отображения окружности: линии бифуркаций удвоения не располагаются внутри языка, а обрываются на его краях в точках бифуркаций коразмерности два. Как оказывается, при последовательных удвоениях периода они сходятся к точке, классифицируемой как критическая точка типа С: S=-0.548966, J=1.547188.

О треугольники устойчивости см. С.П.Кузнецов. Динамический хаос, с. 213. Описание и свойства универсального отображения, включая особенности устройства языков синхронизации, см. в статье А.П.Кузнецова, А.Ю.Кузнецовой и И.Р.Сатаева "О критическом поведении отображения с бифуркацией Неймарка - Сакера при разрушении фазовой синхронизации в предельной точке фейгенбаумовского каскада", 2003 г.

главная наука атлас только эта страница в начало

Саратовская группа
теоретической нелинейной
динамики