Простые примеры странных нехаотических аттракторов

В современной нелинейной динамике на равноправной основе рассматривают системы с непрерывным и с дискретным временем. Первые задаются дифференциальными уравнениями, вторые - итерируемыми отображениями. Чтобы СНА мог реализоваться в системе с непрерывным временем, в дифференциальном уравнении должна присутствовать квазипериодическая зависимость коэффициентов от времени, что требует наличия как минимум двух несоизмеримых частот. В системах, заданных отображениями, есть собственный внутренний "ритм" - шаги дискретного времени, так что для добавляемого внешнего воздействия достаточно одной частоты, несоизмеримой с частотой шагов. Простейший класс систем, демонстрирующих СНА, - отображения с одной координатной и одной фазовой переменной. При этом внешнее воздействие характеризуется одним частотным параметром, который при проведении конкретных исследований чаще всего полагают равным "золотому среднему" - числу (5^1/2-1)/2.

Замечание. Этот выбор обусловлен не только упрощением теоретического анализа, на что обычно ссылаются, но также и тем, что тонкие структуры, выявление которых составляет предмет экспериментов и численных расчетов, оказываются лучше различимыми, чем это имеет место при других соотношениях частот.

Модель с бифуркацией вилки

Возьмем отображение x_n+1=lth x_n, которое демонстрирует бифуркацию вилки: при l<1 аттрактором служит неподвижная точка в нуле, при l>1 она становится неустойчивой, но появляются две симметрично расположенных устойчивых точки x=±x₀(l). Следуя работе Grebogi et al., модифицируем его, введя квазипериодическую зависимость коэффициента от дискретного времени:

где q - фазовая переменная. Параметр w=(5^1/2-1)/2 определяет частоту внешнего воздействия, которое носит в данном случае мультипликативный характер. Вычислим показатель Ляпунова для решения x=0. В линейном приближении

и

В силу иррациональности w, значения фазы q_n при N® ¥ равномерно и плотно распределены на единичном интервале. Поэтому сумму заменяем интегралом, и для показателя Ляпунова имеем

При l<1 получаем L<0, т.е. решение устойчиво, и линия x=0 на плоскости (q,x) служит аттрактором. При l>1 оно характеризуется положительным показателем Ляпунова и аттрактором не является.

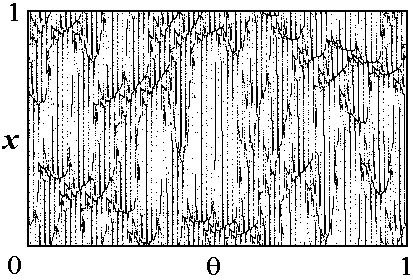
Что можно сказать об аттракторе при l>1? Во-первых, он непременно содержит точки с |x|>0. Во-вторых, поскольку |th x|<1, аттрактор расположен в полосе |x|<2l. В-третьих, на оси x=0 присутствует множество точек, принадлежащих аттрактору. В самом деле, при q=1/4 косинус обращается в ноль, так что для всех q_n=1/4+nw, где n=1, 2,...,¥ имеем x_n=0. Это подмножество точек аттрактора бесконечное и всюду плотное, так что аттрактор в целом представляет собой заведомо нетривиальный геометрический объект, "странное" множество. На рисунке представлены изображения СНА в рассматриваемой системе, фазовый портрет на плоскости и итерационная диаграмма в координатах (x_n,x_n+1).

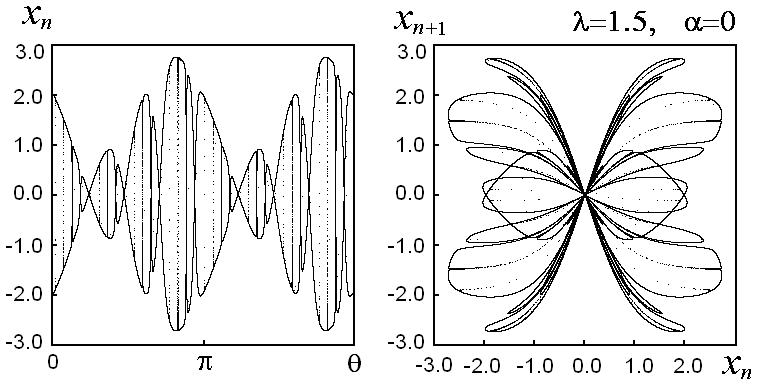
Для данного аттрактора показатель Ляпунова отрицательный. В самом деле, для функции f(x)=th x справедливо соотношение |f'(x)|£|f(x)/x|, причем равенство достигается лишь при x=0. Поэтому для ляпуновского показателя получаем оценку

Квадратичное отображение с квазипериодическим воздействием

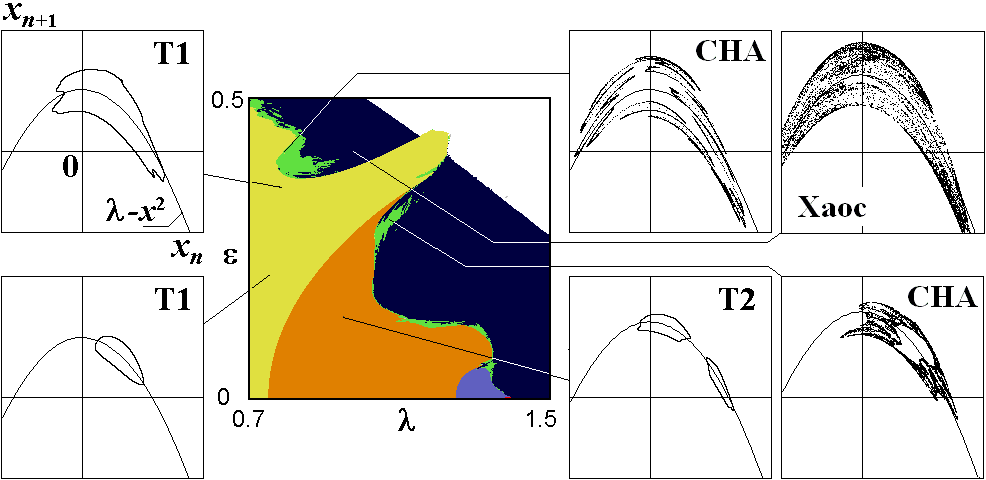
Одна из популярных и содержательных моделей в нелинейной динамике – квадратичное отображение x_n+1=l-x_n², в котором при увеличении параметра l имеет место переход к хаосу через последовательность бифуркаций удвоения периода. Вводя переменную добавку к l, осциллирующую с иррациональной частотой w и амплитудой e, приходим к модели

в которой при некотором выборе параметров возникает СНА. На рисунке показана карта режимов на плоскости параметров (l, e), а по периферии – итерационные диаграммы с портретами аттракторов в нескольких характерных точках. Желтым, оранжевым и голубым обозначены области, где реализуются тор-аттракторы типа Т1, Т2, Т4, изображающиеся на итерационной диаграмме соответствующим количеством замкнутых кривых, зеленым - области СНА, темно синим - хаоса.

Модель с касательной бифуркацией

Рассмотрим отображение x_n+1=f(x_n)+b, где функция f выбрана так, что имеет место касательная бифуркация: при изменении b две неподвижные точки, устойчивая и неустойчивая, сближаются, сливаются и исчезают, оставляя узкий «коридор», прохождение которого требует большого числа итераций. Если динамика после прохождения «коридора», такова, что траектория обязательно вернется к месту входа в него, то возникает тип динамического поведения, известный как перемежаемость. Имея целью локальный анализ бифуркации, функцию можно задать в виде f(x)=x/(1–x). Предполагая, что параметр b содержит квазипериодическую добавку с амплитудой e, приходим к модели

Она пригодна для изучения перехода, являющегося аналогом касательной бифуркации и ведущего к рождению СНА, но для описания СНА, как такового, нуждается в модификации, вводящей механизм возврата. Интересно, что заменой x_n=1–Y_n/Y_n–1 данное уравнение приводится к линейному разностному уравнению Харпера

которое известно в физике твердого тела в контексте анализа локализации и делокализации квантовых состояний в одномерной модели квазипериодической среды.

Отображение окружности с квазипериодическим воздействием

Отображением окружности принято называть модель c дискретным временем x_n+1=x_n+r+(K/2p)sin2px_n, где переменная x_n определена с точностью до целой части («по модулю 1»). Это можно интерпретировать как задачу об автогенераторе, на который действует периодическая последовательность импульсных толчков: x_n определяет фазу колебаний перед n-м толчком, K характеризует интенсивность толчков, а r – отклонение частоты следования импульсов от частоты автоколебаний. Добавляя член, отвечающий дополнительному воздействию с несоизмеримой частотой, приходим к модели

В отсутствие дополнительного члена на плоскости параметров (r,K) можно видеть языки Арнольда, где динамика периодическая, области квазипериодического поведения и хаоса (см. рисунок слева).

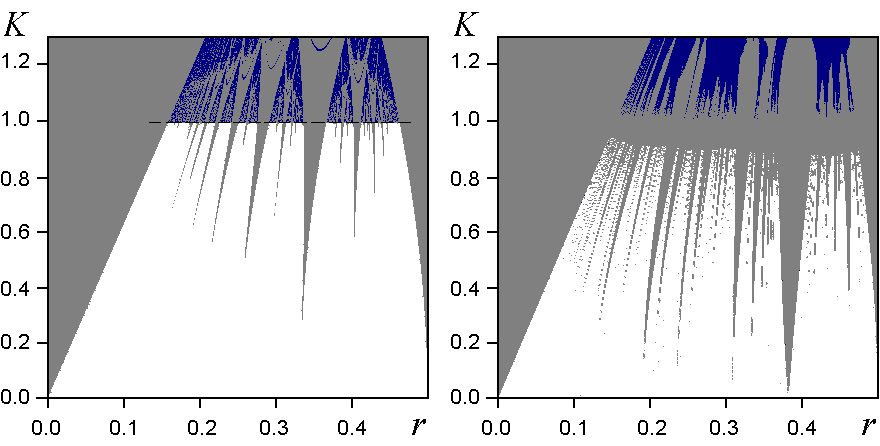
Нижняя часть плоскости параметров, где реализуется регулярная динамика (периодическая и квазипериодическая) и верхняя, где возможен хаос, разграничены критической линией K=1 (пунктир). При включении квазипериодического воздействия вместо критической линии возникает критическая зона (рисунок справа). Ее ширина тем больше, чем больше амплитуда воздействия. Языки Арнольда трансформируются в зоны квазипериодической динамики с двумя несоизмеримыми частотами (частота шагов и частота воздействия), которые отвечают аттракторам в виде двумерных торов, а области между языками соответствуют теперь трехчастотной квазипериодичности или трехмерным торам (добавляется частота «прокручивания» циклической переменной x). Ниже критической зоны присутствуют указанные два типа регулярной динамики. Выше нее имеются области хаоса. Наконец, в самой критической зоне в зависимости от параметров могут реализоваться двухчастотная квазипериодичность или СНА (см. пример на рисунке внизу для e=0.6, K=1, r=0.3, w=(5^1/2-1)/2).