Системы с непрерывным временем и эксперименты по наблюдению СНА

До сих пор мы обсуждали модели с дискретным временем, представленные итерируемыми отображениями. Рассмотрим вопрос о возможности реализации СНА в системах, заданных привычными физикам дифференциальными уравнениями. Ключевой момент - установление связи между дифференциальными уравнениями и описанием динамики в терминах отображений на основе идеи сечения Пуанкаре для интересующего нас класса систем с квазипериодическим воздействием.

Предположим для определенности, что система без внешнего воздействия имела двумерное фазовое пространство (x, y) и описывалась двумя дифференциальными уравнениями первого порядка. В случае двухчастотного воздействия функции в правых частях уравнений надо считать зависящими периодическим образом от фазовых переменных Q и F, изменяющихся во времени по линейному закону:

причем частоты w и W полагаем находящимися в иррациональном отношении. Пусть в момент, отвечающий определенной фазе второй составляющей F, имеем значения переменных (x, y, Q); какими они будут через один период этой составляющей T=2p/W? Из теоремы единственности решения дифференциального уравнения следует, что эти величины должны однозначно выражаться, как некоторые функции от исходных значений. Еще через период они получатся повторным применением тех же функций и т.д. Итак, возникает итерируемое отображение

С формальной точки зрения, мы имеем сечение четырехмерного фазового пространства (x, y,Q,F) гиперплоскостью F=const, и можем говорить об отображение этой гиперплоскости в себя. (Так как по F фазовое пространство имеет периодическую структуру, можно не различать точки, отстоящие друг от друга на целое число периодов T.) В данном контексте это и есть отображение Пуанкаре или стробоскопическое отображение.

Теперь можно отвлечься от исходных дифференциальных уравнений и сосредоточиться на анализе динамики, порождаемой отображением Пуанкаре. Эта подмена объекта исследования не сопровождается приближениями, анализ остается точным. Цена, которую приходится заплатить, – это потеря информации о характере динамики в промежутки времени между последовательными пересечениями секущей поверхности, в частности, о продолжительности интервалов времени между ними и о топологических свойствах фазовых траекторий. Тем не менее, сохраняется возможность анализировать существенные вопросы, например, реализуется в системе регулярный режим, хаос, или СНА.

Чаще всего, функции F₁ и F₂ можно получить только на основе численного решений системы дифференциальных уравнений. Однако, с принципиальной точки зрения, мы имеем задачу того же типа, что и модели с дискретным временем – отображения с квазипериодическим воздействием. Добавим, что в системах с сильной диссипацией наблюдаемые по ходу временной эволюции состояния на секущей гиперплоскости имеют тенденцию располагаться при каждом фиксированном Q вдоль одномерной кривой на плоскости (x, y). В этом случае, введя вместо пары переменных (x, y) одну координату, отсчитываемую вдоль этой кривой, приходим к описанию динамики в терминах одномерного отображения с квазипериодическим воздействием.

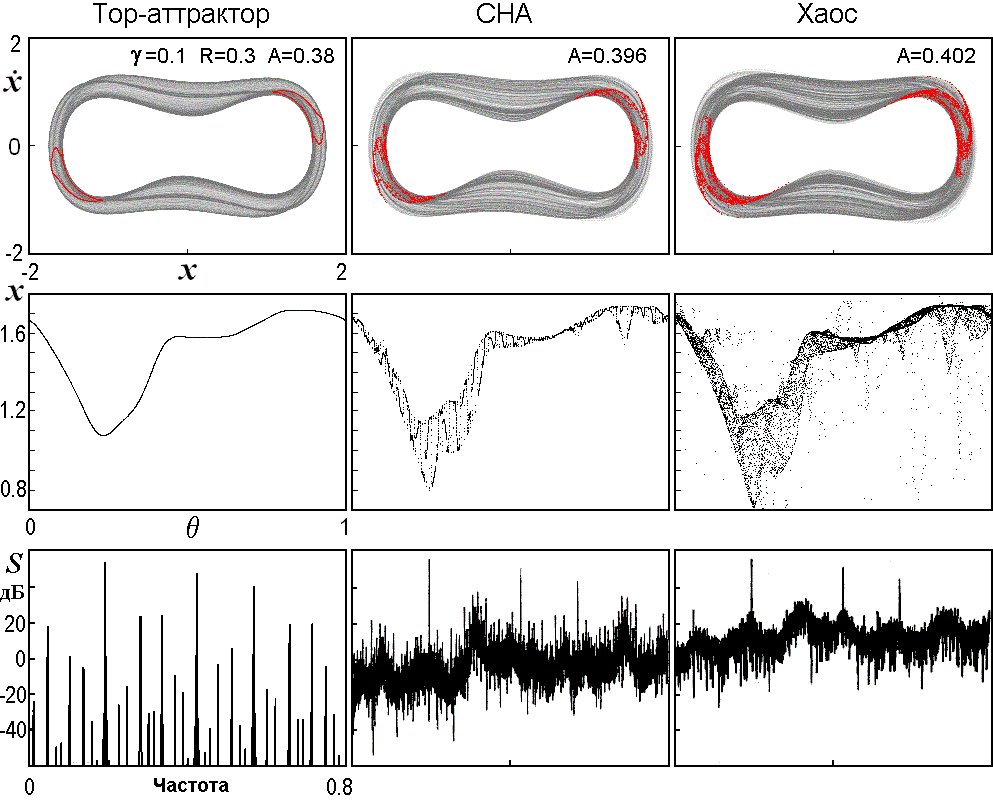
Представительный и широко исследуемый класс нелинейных систем, демонстрирующих СНА, составляют нелинейные диссипативные осцилляторы, возбуждаемые квазипериодической силой. В качестве примера, на рисунке внизу приводятся численные результаты, относящиеся к нелинейному осциллятору Дуффинга с квазипериодическим параметрическим возбуждением (Heagy and Ditto, J.Nonlinear Sci., 1, 1991, 423):

где w=2p, W=p(5^1/2-1)/2. Показаны фазовые портреты аттракторов в проекции на плоскость (x, y=dx/dt), где красные точки отвечают стробоскопическому сечению F=0, а также фазовые портреты на плоскости (q=Q/2p, x) в сечении Пуанкаре F=0, и спектры Фурье для режимов, соответствующих тору-аттрактору, СНА и хаосу. Численные расчеты показывают, что в данной системе реализуются многие из феноменов, упоминавшихся в предыдущих разделах, в том числе последовательности удвоения торов, переходы к СНА по Хеги-Хэмелу, Нишикава-Канеко, перемежаемость.

Первый описанный в литературе эксперимент по наблюдению СНА в реальной физической системе относится к механическому осциллятору в виде закрепленной на конце магнитно-упругой ленты, колебания которой возбуждаются переменным магнитным полем (Ditto at al., Phys.Rev.Lett., 65, 1990, 533). Система описывается неавтономным уравнением Дуффинга. Режим СНА идентифицировался по виду фазовых портретов в стробоскопическом сечении, скейлинговому поведению составляющих в спектре Фурье, характерному для сингулярно-непрерывного спектра, и по размерностным характеристикам: оценки фрактальной и информационной размерности аттрактора в сечении Пуанкаре дали результаты, близкие, соответственно, к 2 и 1. Сообщалось об обнаружении СНА при численном решении задачи о квазипериодическом воздействии на систему автоколебательного типа – осциллятор Ван-дер-Поля (Kapitaniak et al., J.Phys. A: Math.Gen., 23, 1990, L383), в экспериментах с нелинейными осцилляторами в виде электронных схем, которые представляли собой аналоговые устройства, реализующие динамику, описываемую определенными дифференциальными уравнениями (Zhou et al., Phys.Rev. A45, 1992, 5394; Yu et al., J. Korean Phys. Soc., 34, 1999, 130). Помимо фазовых портретов, спектров и оценки размерностей, представлены дополняющие их результаты, относящиеся к показателям Ляпунова для дифференциального уравнения, аналоговой моделью которого служит исследуемая схема. Во второй из указанных работ целенаправленно реализован и изучен в эксперименте переход к СНА через бифуркацию «blowout».

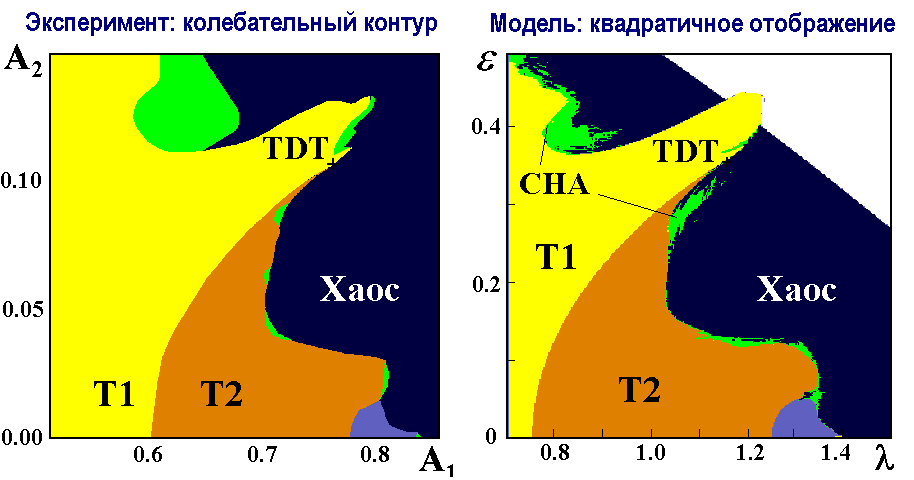
В работе Безручко, Кузнецова и Селезнева (Phys.Rev. E62, 2000, 7287) исследован экспериментально электронный осциллятор в виде возбуждаемого квазипериодически нелинейного колебательного контура, в котором роль нелинейного элемента выполнял полупроводниковый диод. Известно, что при одночастотном возбуждении в этой системе имеет место переход к хаосу через последовательность удвоений периода, как в логистическом отображении. Добавление второй составляющей воздействия на частоте, находящейся с первой в иррациональном отношении (золотое среднее), приводит к появлению тех же феноменов, которые имеют место в квадратичном отображении с квазипериодическим воздействием. В этом можно убедиться, сравнивая приведенные на рисунке карты динамических режимов, одна из которых получена в эксперименте с нелинейным контуром (по осям координат – амплитуды составляющих воздействующего переменного напряжения в вольтах), а вторая из численных расчетов для квадратичного отображения.

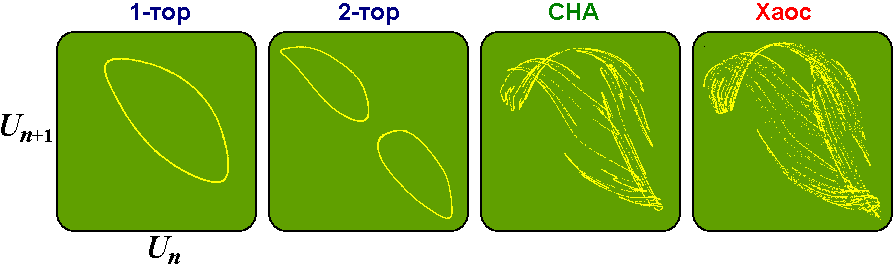
Для идентификации СНА в эксперименте использовалась идея Пиковского и Фойдель: соотношение частот задавалось как рациональная аппроксимация золотого среднего (13/21), и при фиксированных остальных параметрах отслеживалось присутствие или отсутствие бифуркаций в экспериментальной системе в зависимости от соотношения фаз частотных составляющих.

Показаны также полученные в эксперименте фазовые портреты типичных аттракторов (тор, удвоенный тор, СНА, хаос). Для их построения снимаемые с последовательно включенного в контур резистора значения потенциала вводились в компьютер с помощью аналого-цифрового преобразователя, и на графике по осям координат откладывались величины, относящиеся к определенному моменту в пределах n-го и n+1-го периодов основного воздействия.