теоретической нелинейной динамики
Взаимная синхронизация
трех связанных осцилляторов
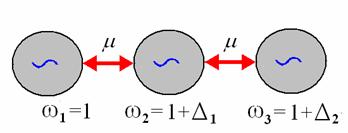
Система трех диссипативно связанных в цепочку осцилляторов
Ван-дер-Поля описывается уравнениями
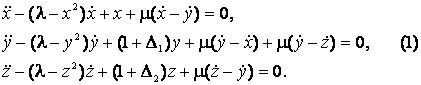
Здесь ![]() – параметр возбуждения
автономных осцилляторов,
– параметр возбуждения
автономных осцилляторов, ![]() – частотная расстройка
второго осциллятора относительно первого,
– частотная расстройка
второго осциллятора относительно первого, ![]() – третьего
относительно первого,
– третьего
относительно первого, ![]() – коэффициент
диссипативной связи. Частота первого осциллятора принята за единицу.
– коэффициент
диссипативной связи. Частота первого осциллятора принята за единицу.
Фазовое приближение
В рамках традиционных
предположений о малости параметров система (1) может быть приближенно приведена
к фазовым уравнениям:
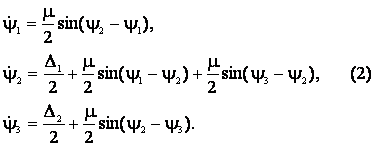
Размерность
системы (2) может быть понижена на единицу, если ввести относительные фазы
осцилляторов ![]() ,
, ![]() . Тогда получаем
. Тогда получаем
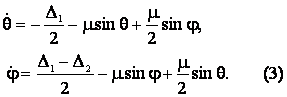
Фазовые
портреты и простейшие режимы
Фазовые
портреты и, соответственно, основные типы режимов аналогичны случаю возбуждения двух
осцилляторов внешним сигналом. Отличия состоят в интерпретации наблюдаемых режимов, которая
определяется физическим смыслом фазовых переменных ![]() и
и ![]() , как относительных фаз
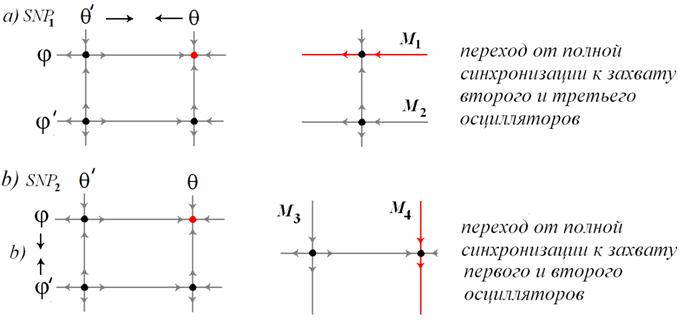
осцилляторов. Рисунок (a) относится к случаю полной синхронизации всех трех
осцилляторов. Можно видеть соединенных гетероклиническим контуром четыре состояния
равновесия, из которых одно устойчиво. Случай (b) отвечает бифуркации SNP, когда состояния равновесия попарно
сливаются, и из их многообразий возникают устойчивая и неустойчивая
инвариантные кривые. Рисунок (d) отвечает двухчастотной квазипериодичности с числом вращения
, как относительных фаз
осцилляторов. Рисунок (a) относится к случаю полной синхронизации всех трех
осцилляторов. Можно видеть соединенных гетероклиническим контуром четыре состояния
равновесия, из которых одно устойчиво. Случай (b) отвечает бифуркации SNP, когда состояния равновесия попарно
сливаются, и из их многообразий возникают устойчивая и неустойчивая
инвариантные кривые. Рисунок (d) отвечает двухчастотной квазипериодичности с числом вращения ![]() . В этом случае в
установившемся режиме фаза
. В этом случае в
установившемся режиме фаза ![]() осциллиирует около некоторого равновесного
значения, что означает частичный
взаимный захват первого и второго осцилляторов. Последний рисунок (d) отвечает режиму трехчастотной квазипериодичности.
осциллиирует около некоторого равновесного
значения, что означает частичный
взаимный захват первого и второго осцилляторов. Последний рисунок (d) отвечает режиму трехчастотной квазипериодичности.

Полная синхронизация трех осцилляторов
Условия
полной синхронизации трех осцилляторов могут быть найдены аналитически. В этом случае
![]() , так что из (3) следуют выражения для относительных фаз:
, так что из (3) следуют выражения для относительных фаз:
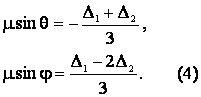
Отсюда
следуют уравнения границ области захвата:
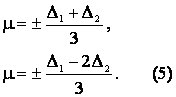
Фиксируем
расстройку ![]() , и изучим устройство плоскости частотная расстройка второго
осциллятора
, и изучим устройство плоскости частотная расстройка второго
осциллятора ![]() – величина связи
– величина связи ![]() . На этой плоскости условия (5) задают линии, показанные на
рисунке.
. На этой плоскости условия (5) задают линии, показанные на
рисунке.
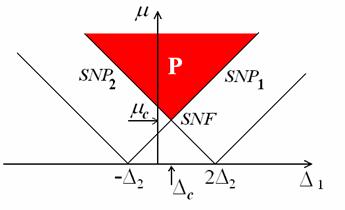
Они
определяют два языка традиционного вида с вершинами в точках ![]() ,
, ![]() Нетрудно показать, что
в терминах частот исходных осцилляторов вершины языков задаются условиями:
Нетрудно показать, что
в терминах частот исходных осцилляторов вершины языков задаются условиями:
![]()
Они
имеют простой физический смысл. Действительно, при диссипативной связи частота
захвата двух осцилляторов равна среднему арифметическому из их собственных
частот. Поэтому условие (a) отвечает
ситуации, когда частота захвата кластера
из второго и третьего осцилляторов, как единого целого, равна частоте первого
осциллятора. Условие (b) отвечает
тому, что частота кластера из первого и второго осцилляторов равна частоте
третьего осциллятора.
Область
полной синхронизации отвечает пересечению двух языков (5) и показана на рисунке
красным цветом. При выходе через ее правую границу ![]() состояния равновесия
попарно сливаются, и возникает режим частичного захвата второго и третьего
осцилляторов (а). При выходе через левую границу
состояния равновесия
попарно сливаются, и возникает режим частичного захвата второго и третьего
осцилляторов (а). При выходе через левую границу ![]() возникает режим
частичного захвата первого и второго осцилляторов (b).
возникает режим
частичного захвата первого и второго осцилляторов (b).
Пересечение
линий ![]() и
и ![]() дает точку
коразмерности два saddle node fan SNF. Ее находим, совмещая оба уравнения (5):
дает точку
коразмерности два saddle node fan SNF. Ее находим, совмещая оба уравнения (5):
![]()
Эти
значения отмечены стрелочками на рисунке. Таким образом, область полной
синхронизации имеет пороговый характер по
величине связи, что отличает обсуждаемую ситуацию от случая двух связанных
осцилляторов.
От языка Арнольда – к
картине синхронизации квазипериодичности
Для двух
связанных осцилляторов на плоскости параметров частотная расстройка – величина
связи реализуется классический язык Арнольда, погруженный в область
двухчастотной квазипериодичности. Для трех связанных осцилляторов на смену
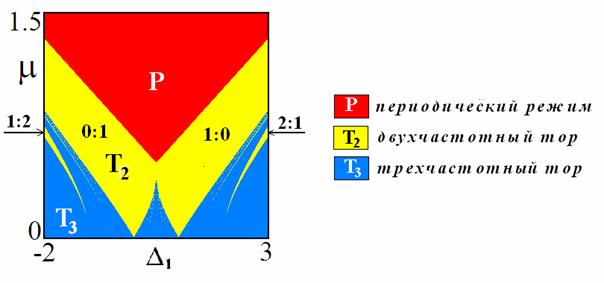
приходит картина, показанная на следующем рисунке. Он представляет собой карту
ляпуновских показателей для фазовой системы (3). На ней указаны области
полной синхронизации, двух- и трехчастотной квазипериодичности и подписаны
числа вращения наиболее представительных режимов.
Область
точного захвата всех трех осцилляторов P отвечает аналитическому рассмотрению. Области
двухчастотных торов имеют вид языков, погруженных в область трехчастотных
торов. Острия этих языков лежат на оси частотной расстройки. При этом в области
малой связи в нижней части карты доминируют режимы трехчастотной
квазипериодичности.
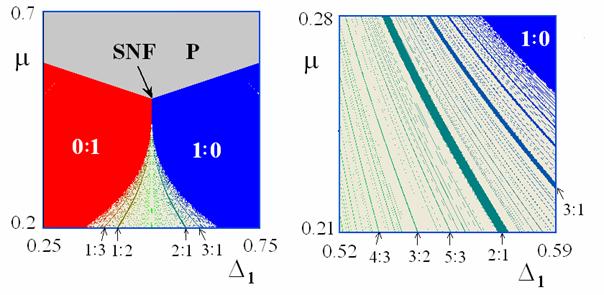
Следующий рисунок представляет
собой карту торов и ее
выделенный фрагмент в окрестности точки SNF. Можно видеть систему языков резонансных
двухчастотных режимов высшего порядка, пронизывающих область трехчастотной
квазипериодичности.
Три связанных осциллятора Ван-дер-Поля
Обратимся теперь к исходной
системе (1). В этом случае картина наблюдаемых режимов будет зависеть от
дополнительного управляющего параметра ![]() . Выберем его значение
не большим
. Выберем его значение
не большим ![]() , что позволит сопоставить полученные результаты с фазовым
приближением.
, что позволит сопоставить полученные результаты с фазовым
приближением.
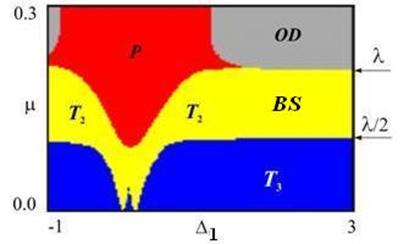
На карте ляпуновских
показателей в области малой связи устройство плоскости параметров соответствуют
фазовому приближению. Однако с увеличением связи наблюдаются существенные отличия.
Во-первых, в области![]() возникает режим
«гибели колебаний» OD
(oscillator death),
который обусловлен тем, что диссипативная связь настолько велика, что подавляет
автоколебательные свойства осцилляторов.
возникает режим
«гибели колебаний» OD
(oscillator death),
который обусловлен тем, что диссипативная связь настолько велика, что подавляет
автоколебательные свойства осцилляторов.
Во-вторых, в интервале ![]() наблюдается новый тип
режима – широкополосная двухчастотная синхронизация BS (broadband synchronization). В
этом случае двухчастотные колебания наблюдаются при сколь угодно большой
частотной расстройке
наблюдается новый тип
режима – широкополосная двухчастотная синхронизация BS (broadband synchronization). В
этом случае двухчастотные колебания наблюдаются при сколь угодно большой
частотной расстройке ![]() . Режимы такого типа
характерны для связанных осцилляторов с неидентичными управляющими
параметрами (Kuznetsov A.P., Roman Ju. P).
. Режимы такого типа
характерны для связанных осцилляторов с неидентичными управляющими
параметрами (Kuznetsov A.P., Roman Ju. P).
Kuznetsov A.P., Roman Ju. P. Properties of synchronization in the systems of
non-identical coupled van der Pol and van der Pol–Duffing oscillators.
Broadband synchronization // Physica D238, 2009, No 16, p. 1499-1506.
Их природа состоит в
доминировании одного, наименее подавленного связью осциллятора. Появление таких
режимов в цепочке идентичных осцилляторов кажется несколько парадоксальным.
Причина состоит в следующем. Обратимся к системе (1) и «выключим» воздействие
остальных осцилляторов на данный. (Это можно реализовать, например, расстроив
существенным образом осцилляторы по частоте.) Тогда первый и третий осцилляторы
будут характеризоваться эффективным управляющим параметром ![]() , а второй –
, а второй – ![]() . Таким образом, центральный
осциллятор продемпфирован связью в два раза сильнее. Причина состоит в
геометрии цепочки: центральный осциллятор испытывает трение со стороны двух
соседей, в то время как крайние – только одного. В результате в области
. Таким образом, центральный
осциллятор продемпфирован связью в два раза сильнее. Причина состоит в
геометрии цепочки: центральный осциллятор испытывает трение со стороны двух
соседей, в то время как крайние – только одного. В результате в области ![]() центральный осциллятор сильно подавлен связью
и легко захватывается соседями, так что возникает характерный режим широкополосной
синхронизации.
центральный осциллятор сильно подавлен связью
и легко захватывается соседями, так что возникает характерный режим широкополосной
синхронизации.
Литература
1. Кузнецов А.П., Сатаев И.Р., Тюрюкина
Л.В. Синхронизация и
многочастотные колебания в цепочке фазовых осцилляторов. Нелинейная динамика,
2010, №4, с. 693-717
2. Кузнецов А.П., Сатаев И.Р., Тюрюкина
Л.В. На пути к многомерным
торам. Изв. Вузов. Прикладная нелинейная динамика. Т. 18, 2010, №6, с. 65-84.
