
Говоря о классической динамике вообще и о динамическом хаосе в частности, мы постоянно опираемся на понятие фазового пространства. Поведение индивидуальной системы представляется движением изображающей точки по фазовой траектории. Динамика ансамбля (множества невзаимодействующих систем, различающихся начальными условиями) интерпретируется как эволюция облака изображающих точек в фазовом пространстве и описывается функцией распределения, уравнение для которой известно в классической механике как уравнение Лиувилля.
В силу принципа неопределенности, в квантовой теории нельзя использовать функцию распределения f(p,x), поскольку мы не вправе конструировать ансамбль из систем, обладающих одновременно импульсом p и координатой x.
Одна возможность построить квантовый аналог функции распределения основана на использовании распределения Хусими, другая - на введении функции Вигнера.
Распределение Хусими
Для квантовой системы фазовую плоскость можно мыслить как набор ячеек размера DpDx=h/2p и говорить о вероятности пребывания в той или иной ячейке. Определить ее можно через интеграл перекрытия волновой функции |y> с когерентным состоянием |ypx>, центрированным в данной точке (p,x). Построенная таким образом функция двух переменных fH(p,x)=|<ypx|y >|2 называется распределением Хусими (Husimi distribution). Ясно, что в классическом пределе, когда h стремится к нулю, гауссов пакет минимальной неопределенности превращается в дельта-функцию, а распределение Хусими в классическую функцию распределения.
Примечание: что такое "когерентное состояние"? По Глауберу, определяют сначала когерентное состояние центрированное в начале координат |y0>, как собственный вектор оператора a=(x+ip)/21/2 с нулевым собственным числом. Соответствующее уравнение в координатном представлении имеет вид xy+(h/2p)dy/dx=0, откуда yµexp(-x2/2ph). Далее строятся состояния, смещенные по импульсу и координате на произвольные величины p и q: |ypq=exp((p+iq)a)|y0. Для отображений на торе, следуя Сарасено, целесообразно использовать разностный аналог оператора a и определить центрированное в начале координат состояние уравнением (A-A++i(K-K+))|y0>=0. Состояния, смещенные на p позиций по импульсу и q позиций по координате, могут быть получены с помощью оператора K+qAp.
Ниже на рисунке представлена эволюция во времени функции Хусими для квантового отображения кота Арнольда при N=131. Начальное состояние отвечает гауссову волновому пакету максимальной локализации. Различные тона серого цвета кодируют уровень функции fH(p,x). Начальная стадия эволюции гауссова пакета демонстрирует очевидное сходство с картинками преобразования изображения кота в классическом случае. Когда ширина пакета становится больше пространственного периода, волновая функция формируется как результат наложения и интерференции "хвостов", протянувшихся из разных периодов: в произвольной точке x она вычисляется как сумма комплексных амплитуд, отвечающих всем точкам пересечения "хвостов" с линией x=const. Как результат этой квантовой интерференции, на последних "кадрах" можно видеть чередующиеся светлые и темные пятна.

Функция Вигнера
Для квантовой частицы, совершающей одномерное движение, функция Вигнера определяется через волновую функцию y
(x): 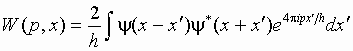
Как нетрудно проверить, величина W(p,x) всегда действительна. Функция Вигнера широко используется в статистической физике, занимая в теории квантовых систем то место, какое в классической статистике занимала функция распределения. Основанием служит то, что интегрирование функции Вигнера по первому аргументу приводит к распределению вероятностей для координаты, а по второму - для импульса:
![]()
Если на волновую функцию наложены соответствующие тору условия периодичности с единичным периодом по координате и импульсу, то функция Вигнера W представляется, как можно показать, набором дельта-функций в узлах квадратной решетки с шагом 1/2N. Задать ее можно таблицей из 2Nx2N действительных чисел, определяющих амплитуды дельта-пиков:
![]()
где индексы k и m принимают целые и полуцелые значения (0, 1/2, 1, 3/2,...N-1/2).
Суммирование w(k,m) по k дает распределение вероятностей в координатном, а суммирование по m - в импульсном представлении:

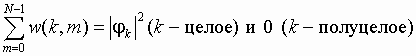
Можно показать, что эволюция функции Вигнера за один шаг дискретного времени в квантовом отображении кота Арнольда выражается простым соотношением
![]()
Иными словами, значения функции Вигнера, приписанные узлам решетки 2Nx2N, просто переносятся без изменения вдоль классических траекторий, порождаемых на этой решетке отображением вида
![]()
Замечание. Добавка 1/2, возникшая в уравнении для k', в каком-то смысле несущественна, поскольку устраняется сдвигом начала отсчета по k и m: m->m-1/2, k->k+1/2. Такое переопределение координат неудобно, поскольку приводит к необходимости работать с полуцелыми индексами, но зато восстанавливает полное соответствие с формой классического отображения.
На рисунке внизу показано эволюция во времени функция Вигнера в квантовом отображении кота Арнольда при N=13. В качестве начального состояния задан гауссов пакет. Эволюция периодическая: возврат к исходному состоянию наступает через 14 шагов. Гиперболическое отображение имеет ту особенность, что на протяжении периода заметно отличные от нуля значения функции более или менее разбредаются по всей площади квадрата.

теоретической нелинейной
динамики