|
Description
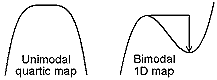
1D maps
The period-doubling accumulation point in unimodal map of 4-th power.
For bimodal 1D maps - the limit of period-doubling on a special curve
in the parameter plane defined by the condition "extremum is mapped to
extremum". T-point appears as the terminal point of the Feigenbaum curve. This type of critical behavior is known after Chang, Wortis, Wright, and Fraser and Kapral.
More general systems
T-point may appear generically only in codimension 3. In some cases the
pseudo-tricritical behavior may occur, as an intermediate asymptotics.
RG equation
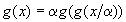
The fixed point
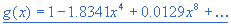
The orbital scaling factor
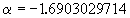
Critical multiplier
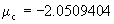
Relevant eigenvalues
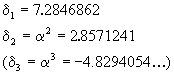
Codimension
CoDim=3 (restr. 2)
|
Codimension-2 example
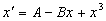
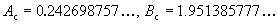
Param. space arrangement and scaling with factors
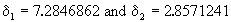
Scaling coordinates
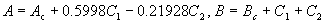
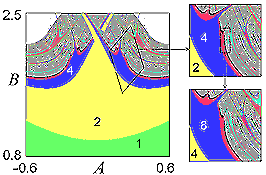
show enlarged figure
Codimension-3 example
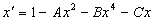 , ,
tricritical point at
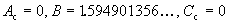
Codimension-3 example in 2D invertible map
 . .
For D=0.3 the tricritical point is located at

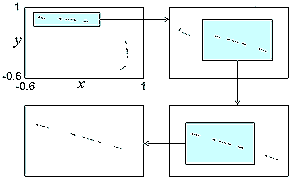
show enlarged figure
|