От решетки диссипативно связанных отображенийк непрерывной среде
Модели
Рассмотрим решетку связанных отображений, заданную уравнением
![]()
где f(x)=1–lx2, n – дискретное время, m – пространственный индекс, L – линейный оператор, осуществляющий усреднение по некоторой пространственной области, притом симметричным образом.
Можно показать, что при такой структуре оператора эволюции, когда он представляется в виде двух последовательно выполняемых преобразований – локального нелинейного и нелокального линейного, связь между ячейками оказывается чисто диссипативной. Два примера такой связи:
![]()
![]()
Диссипативная связь стремится выровнять мгновенные состояния элементов, а когда состояния пространственно близких ячеек решетки становятся близкими, это делает естественным ее описание как непрерывной среды. Время остается дискретным, так что это среда связанных отображений. Для случая “future coupling” имеем
![]()
Параметр D естественно именовать коэффициентом диффузии.
Ренормгрупповой анализ
Обозначим оператор эволюции за один шаг xn+1=G[xn]. Применим его дважды: xn+2=G[G[xn]] и выполним пересчет масштабов динамической переменной и пространственной координаты посредством оператора Sx(z)=ax(21/2z), где a=-2.5029… – константа Фейгенбаума. В силу соотношения D=eh2, перенормировка пространственной координаты на 21/2
отвечает пересчету ответственного за связь члена на фактор 2, т.е. на собственное число, ассоциирующееся с диссипативной связью. В перенормированных переменных имеем xn+2(z)=SG[G[S-1xn]], так что новый оператор эволюции есть G1[x]=SG[G[S-1x]]. Повторяя процедуру многократно, получаем последовательность операторов![]()
причем Gk есть оператор эволюции за 2k временных шагов. Оказывается, что в точке накопления удвоений периода индивидуального отображения l=lс последовательность операторов Gk сходится к неподвижной точке – универсальному оператору, который удовлетворяет операторному уравнению
Если же отойти по параметру l
от критического значения, то возмущение неподвижной точки операторного уравнения будет нарастать как
dk:
Gk[x]@G[x]+c
dkH[x],
где ![]()
Отсюда вытекают следующие свойства универсальности и скейлинга.
Универсальность. Для среды, построенной из дисспативно связанных симметричным образом отображений, демонстрирующих удвоения периода по Фейгенбауму, оператор эволюции за число шагов 2k с точностью до масштабной замены определяется в асимптотике по k одним-единственным параметром Сµl–lс. Скейлинг. Имея некоторый режим пространственно-временной динамики при близком к критической точке значении параметра l , мы должны наблюдать подобную же динамику и при l new=l c+(l –l с)/d. При этом динамическая переменная перенормируется на фактор a, характерный временной масштаб возрастает в 2 раза, а пространственный в 21/2 раза.
Компьютерные иллюстрации свойства скейлинга
Первая серия рисунков, относится к решетке связанных отображений со связью “future coupling”
![]()
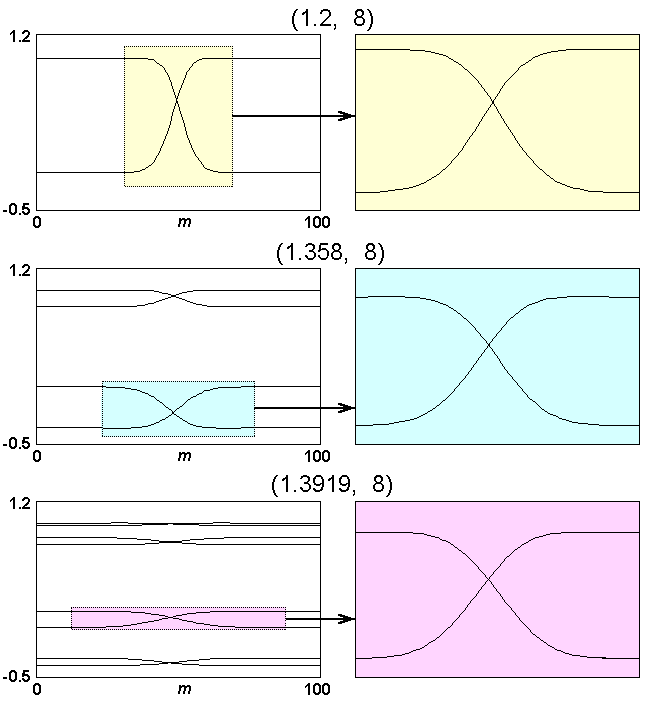
и на них представлены зависимости динамической переменной от пространственной координаты в разные моменты времени. Первая картинка отвечает l=1.2, так что временной период равен 2. При этом начальные условия заданы так, что образовалась “доменная стенка” – область, разделяющая два участка среды, где элементы совершают колебания в противофазе. Ширина этой стенки определяется заданным коэффициентом диффузии, D=8. Справа отдельно показан фрагмент картинки, собственно доменная стенка. Второй рисунок получен при значении параметра, пересчитанном по правилу lnew=lc+(l –l с)/d , и с тем же коэффициентом диффузии. При этом реализуется уже режим с временным периодом 4. Фрагмент картинки справа соответствует изменению масштаба по вертикали на фактор a, а по горизонтали на фактор 2-1/2 по сравнению с предыдущим рисунком. Третий рисунок отвечает еще одному шагу пересчета масштабов. Свойство скейлинга проявляется в том, что конфигурации на диаграммах справа визуально неотличимы.
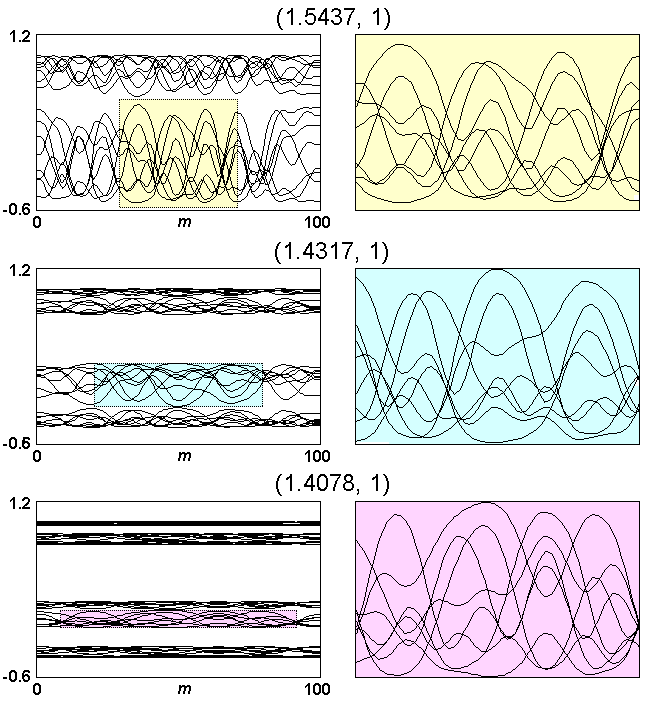
Вторая серия рисунков, относится к закритической области, когда пространственно-временная динамика хаотическая. Первая картинка соответствует l=1.5437, вторая и третья – значениям параметра, пересчитанным по указанному выше правилу. Коэффициент диффузии D=1. В силу присущей хаотическому режиму неустойчивости по отношению к малому возмущению начальных условий, трудно ожидать точного совпадения картинок при масштабном пересчете, тем не менее, можно усмотреть подобие в более общем, статистическом смысле. Очевидно соответствие общего характера зависимостей, в частности, масштабов вариации переменной по амплитуде и координате.
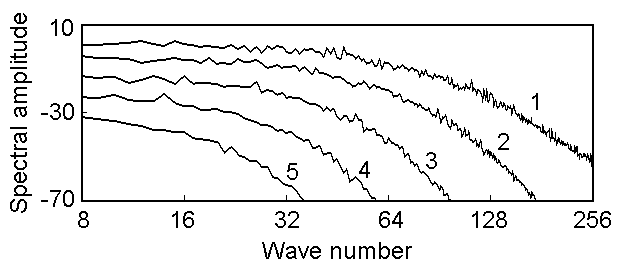
Для количественного подтверждения скейлинга можно сопоставить статистические характеристики (спектры, корреляционные функции) подобных друг другу режимов. В качестве примера приводятся пространственные спектры, в двойном логарифмическом масштабе. Кривые 1-3 соответствуют режимам с предыдущего рисунка, а 4 и 5 – следующим уровням скейлинга. Свойство скейлинга выражается в том, что кривые совмещаются друг с другом при сдвиге на некоторое расстояние по горизонтальной оси (пересчет масштаба пространственной координаты) и по вертикальной (перенормировка амплитуды).
Универсальный паттерн у края системы и скейлинг, связанный с конечными размерами среды
Рассмотрим решетку достаточно большой длины с фиксированным граничным условием на левом конце xn(0)=0 при критическом значении параметра lc=1.401155189…:
![]()
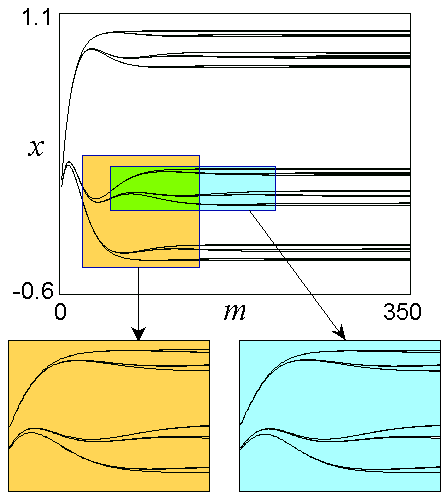
На верхней диаграмме можно видеть структуру, формирующуюся у края системы, а на двух других – фрагменты этой структуры. Масштабы на втором и третьем графиках по горизонтальной оси отличаются на фактор 21/2, а по вертикали на фактор а. Обратите внимание на замечательное соответствие “желтой” и “синей” панелей, отвечающих двум уровням скейлинга. Структура содержит иерархию "хвостов”, отвечающих разным уровням удвоений периода, причем хвосты каждого последующего уровня в 21/2 раз длиннее.
В системе конечной длины, например, с граничными условиями xn(0)=xn(m)=0, хвосты образуются у обоих краев. Если отслеживать изменение режима в зависимости от параметра, то хвосты, формирующиеся при первых удвоениях периода, будут иметь относительно небольшую длину, но она увеличивается в 21/2 раз при каждом последующем удвоении временного периода. Когда длина хвостов сравняется по порядку величины с длиной системы, конечный размер начнет существенным образом сказываться на бифуркациях удвоения, т.е. они будут сдвинуты по параметру относительно невозмущенных, отвечающих точечной системе (или безграничной среде).
Для бифуркаций удвоения в конечной системе имеет место соотношение
![]()
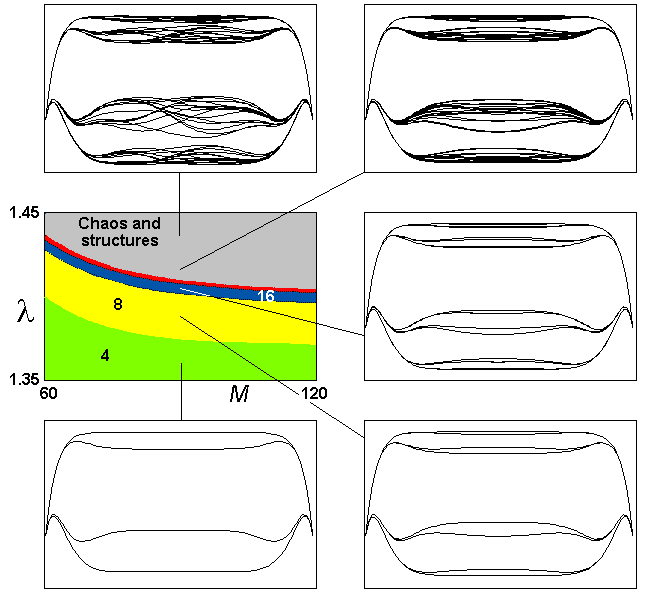
где D - константа, определяющая положение центра подобия системы "хвостов" и зависящая от конкретного вида граничных условий. На следующем рисунке приведена карта режимов и пространственные диаграммы, иллюстрирующие характер изменения структур при переходе к хаосу. Обратите внимание, что хаос возникает в середине отрезка среды; сначала он, очевидно, конечномерный (пространственная структура однотипна в разные моменты времени), а затем включается большее число пространственных мод (см. диаграмму слева вверху).
Саратовская группа