
на фейгенбаумовский
тип поведения
 |
Действие шума на фейгенбаумовский тип поведения |
Сценарий перехода к хаосу через удвоения по Фейгенбауму имеет место в огромном количестве систем, например, в моделях Ресслера и Лоренца, отображениях Эно и Икеды, в отображении окружности внутри языков Арнольда, в колебательном контуре с диодом и других возбуждаемых периодическим воздействием нелинейных осцилляторах, в автоколебательных системах, таких как генератор с инерционной нелинейностью, генератор Дмитриева-Кислова, схема Чуа. В литературе сообщалось также об экспериментальном наблюдении перехода к хаосу по Фейгенбауму при конвекции в жидком гелии и ртути, при акустических колебаниях пузырьков в жидкости, в лазерах с модулированной добротностью, в гибридных акусто-оптических системах с запаздыванием, в системах фазовой автоподстройки частоты, в лампе обратной волны. Этот список можно продолжить.
Если говорить о реальных физических системах, неизбежно присутствующим фактором всегда является наличие шума, который можно рассматривать как случайное внешнее воздействие на систему. Поскольку без шума вблизи точки накопления бифуркаций удвоения периода имеют место обнаруженные Фейгенбаумом универсальные закономерности, можно полагать, что и воздействие шума должно характеризоваться определенными свойствами универсальности и скейлинга. Учитывая ожидаемую универсальность, для поиска соответствующих закономерностей естественно обратиться к простейшей модели, демонстрирующей удвоения периода - квадратичному (логистическому) отображению, в которое добавлено случайное воздействие:
![]()
Здесь xn - последовательность статистически независимых случайных величин с нулевым средним и фиксированным среднеквадратичным значением s, k - параметр, характеризующий интенсивность шума.
Ренормгрупповой (РГ) анализ, предложенный в работах [J.P.Crutchfield et al., 1981] и [Shraiman et al., 1981], приводит к заключению, что существует универсальная константа, которая показывает, во сколько раз надо уменьшить шум для того, чтобы можно было наблюдать каждый новый уровень удвоений периода: g=6.619036513. (Содержание РГ анализа изложено здесь.) Более общая формулировка свойства масштабного подобия (скейлинга) такова:
Предположим, что при каком-то значении параметра l близком
к критической точке Фейгенбаума и при достаточно малом уровне шума
k наблюдается некоторый режим поведения. Тогда при
отклонении от критической точки по параметру l в
Рассмотрим несколько компьютерных иллюстраций указанного свойства скейлинга.
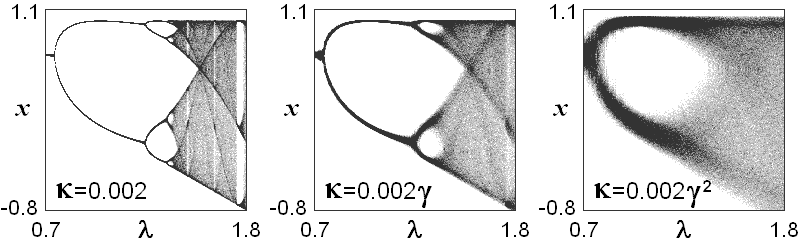
На первом рисунке показаны "бифуркационные деревья" для квадратичного отображения с шумом. По горизонтали отложен управляющий параметр l, а по вертикальной - значения динамической переменной x, пробегаемые в ходе эволюции модели в течение определенного большого числа итераций (с исключением начальной части итераций, отвечающей переходному процессу). Вследствие присутствия шума "ветви" бифуркационного дерева "размазываются", так что высшие бифуркации удвоения становится невозможным различить. Каждая последующая картинка отвечает интенсивности шума увеличенной в g раз по сравнению с предыдущей, и при этом количество различимых бифуркаций удвоения уменьшается как раз на одну.
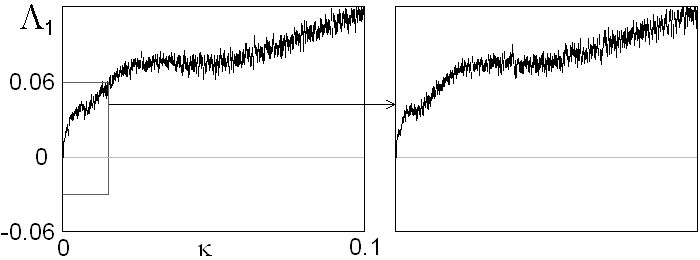
Следующий рисунок иллюстрирует зависимость показателя Ляпунова квадратичного отображения от интенсивности шума при фиксированном l, отвечающем критической точке Фейгенбаума. При уменьшении амплитуды шума на фактор g динамика должна быть подобна исходной в статистическом смысле, но с увеличенным вдвое характерным временем. Это соответствует уменьшенному вдвое показателю Ляпунова. Поэтому график демонстрирует свойство масштабной инвариантности: при увеличении на фактор g по горизонтальной и в 2 раза по вертикальной оси вид зависимости воспроизводится с достаточно хорошей точностью.
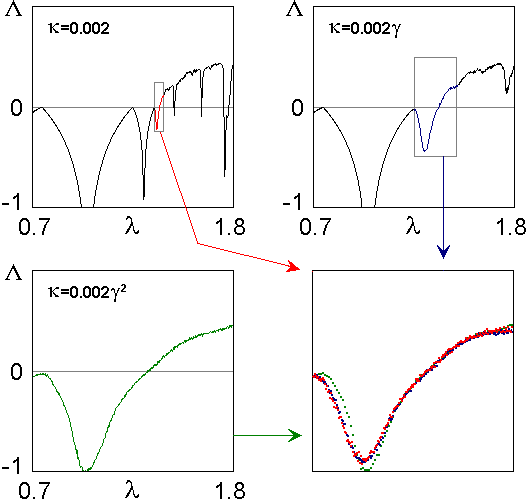
Рассмотрим теперь график показателя Ляпунова в зависимости от параметра l. Выделим небольшой фрагмент картинки вблизи критической точки Фейгенбаума (левая верхняя диаграмма на следующем рисунке). При увеличении амплитуды шума в g раз и пересчете масштаба (т.е. размера выделяемого фрагмента) по горизонтали в d=4,6692... раз и по вертикали в 2 раза в новых координатах видим, что точки ложатся на одну и ту же кривую.
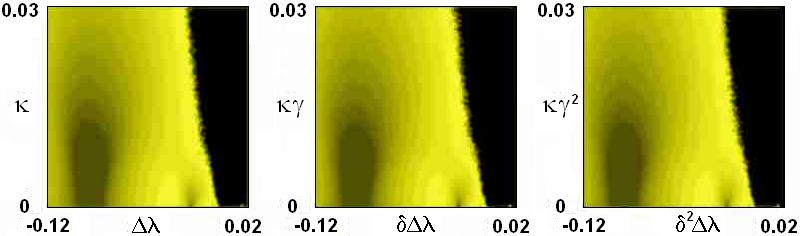
Последний рисунок иллюстрирует свойство скейлинга на карте показателя Ляпунова. По горизонтальной оси отложен параметр l, а по вертикальной - параметр шума e. Для каждого элемента графического изображения, отвечающего определенным l и e вычисляется показатель Ляпунова, и соответствующий пиксель кодируется цветом - тонами от темного к светлому для значений от минус бесконечности до нуля, и черным для положительных значений. Для каждой последующей диаграммы этой серии производится пересчет масштаба на фактор d по горизонтальной оси и g по вертикальной. Одновременно переопределяется правило кодирования показателей Ляпунова цветом, так чтобы учесть уменьшение их характерного масштаба вдвое. Как можно видеть, полученные картинки с достаточной степенью точности соответствуют друг другу, что подтверждает ожидаемое свойство скейлинга.
Замечание. При проведении численных расчетов для величин xn принималось равномерное распределение в интервале от -0.5 до 0.5, тогда s=1/12. Конкретное предположение о свойствах распределения не является существенным, так как для других распределений результаты должны быть эквивалентными из-за ожидаемой универсальности. Неприятное свойство гауссова распределения с точки зрения компьютерного моделирования процесса состоит в том, что оно имеет "хвосты" формально простирающиеся в бесконечность. При этом возможно, хотя и маловероятно, появление таких случайных "толчков", которые ведут к уходу динамической переменной на бесконечность.