Отображение окружности

это одна из фундаментальных моделей, описывающая многие диссипативные нелинейные системы - автогенератор под периодическим воздействием, контакт Джозефсона в высокочастотном поле, волны плотности пространственного заряда в физике твердого тела, маятник с затуханием под внешним воздействием. В исследованиях, касающихся биологических и медицинских проблем, отображение окружности вводят как модель динамики сердца в присутствии конкуренции двух водителей ритма (пейсмекеров).

Отображение окружности - не только качественная модель, но также представитель класса универсальности, ассоциирующегося с переходом к хаосу через квазипериодическое движение. Наиболее проработан анализ перехода при отношении основных частот или числе вращения «золотое среднее»: w=(5^1/2-1)/2, которому соответствует критическая точка GM, располагающаяся при K=1 и r=r_c=0.60666106347011... Имеется много экспериментов, в которых универсальные закономерности, связанные с этой критической точкой, наблюдались и документированы, например, при конвекции жидкости в присутствии периодического воздействия, в электронных осцилляторах и автогенераторах с квазипериодическим внешним воздействием.

В реальных физических системах неизбежно присутствует шум. Обратимся к отображению окружности, в которое добавлено случайное воздействие:

где x_n - последовательность статистически независимых случайных величин с нулевым средним и фиксированным среднеквадратичным значением s, e - параметр, характеризующий интенсивность шума, который считается малым.

Ниже показаны карты показателя Ляпунова для отображения окружности на плоскости параметров (r, K) без шума (первая диаграмма, где отмечено положение точки GM) и в присутствии шума (вторая и третья диаграммы). Для каждого элемента графического изображения, отвечающего определенным r и K, вычисляется показатель Ляпунова, и соответствующий пиксель кодируется тонами от темного к светлому для значений показателя от минус бесконечности до нуля, и черным для положительных значений. Области периодического поведения в системе без шума называют языками Арнольда - это окрашенные в серый цвет образования в виде острий, внутри которых установившийся режим динамики периодический (рациональные числа вращения). Между ними имеют место квазипериодические режимы (иррациональные числа вращения).

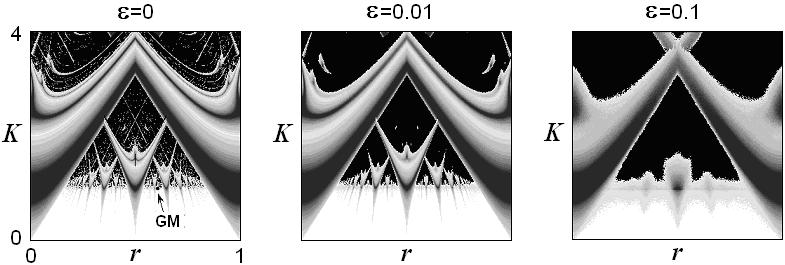
В присутствии шума периодическая или квазипериодическая динамика в точном смысле не реализуется, но картина характерных областей на картах показателя Ляпунова остается видна, по крайней мере, при малых или умеренных шумах. Мы можем говорить о "шумовом периодическом режиме", когда ляпуновский показатель отрицателен, о "шумовом квазипериодическом", когда он близок к нулю, или о "шумовом хаотическом", если показатель Ляпунова положителен. Ляпуновские карты позволяют различать визуально эти режимы. В каком-то смысле, влияние шума выглядит довольно очевидным: тонкие детали картины оказываются "замазаны".

На следующем рисунке представлены фазовые портреты аттракторов на итерационных диаграммах - графиках зависимости x_n+Fk от x_n, где F_k – одно из чисел Фибоначчи. Диаграммы построены для F₆ = 8 при значениях параметров K и r соответствующих критической точке GM в отображении без шума.

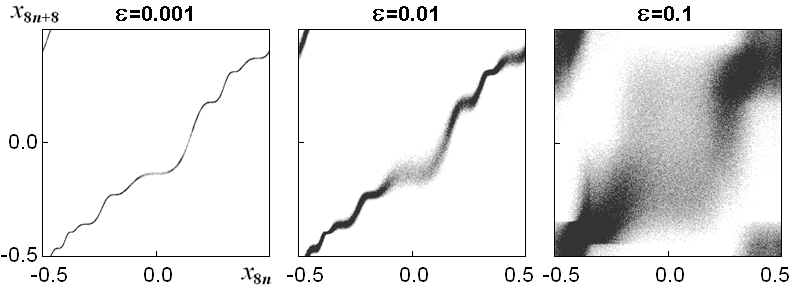
Первая картинка отвечает очень малому шуму, вторая и третья - большей его интенсивности (см. указанные на графиках значения e). Можно видеть, как с увеличением шума последовательно размываются сначала тонкие, а затем более крупные детали структуры аттрактора.

Поскольку без шума вблизи критической точки GM имеют место определенные универсальные закономерности [Shenker, Ostlund, Rand, Feigenbaum, Kadanoff], можно полагать, что и воздействие шума тоже должно характеризоваться какими-то свойствами универсальности и скейлинга. Ренормгрупповой (РГ) анализ, предложенный в работе [Hamm and Graham, 1992] приводит к заключению, что существует универсальная константа, которая показывает, во сколько раз надо уменьшить шум для того, чтобы можно было наблюдать каждый новый уровень мелкомасштабной структуры в окрестности критической точки GM: g=2.3061852653. (Содержание РГ анализа изложено здесь.)

Более общая формулировка свойства масштабного подобия (скейлинга) такова.

Предположим, что при отклонении r от значения, отвечающего числу вращения "золотое среднее" Dr и при каком-то K близком к K_c=1 в присутствии шума e наблюдается некоторый режим поведения. Тогда при Dr уменьшенном в d1=2.83361066 раз, при DK уменьшенном в d2=1.66042438 раз, и уровне шума e/g будет реализоваться статистически подобный режим с характерным временным масштабом в W=1/w=(5^1/2+1)/2 раз большим. При этом закон распределения переменной x вблизи точки перегиба графика отображения будет подобен исходному, с характерным масштабом по x в a=-1.28857455 раз меньше. В области малых отклонений от критичности и малом уровне шума закон распределения, как можно полагать, в значительной мере универсален, т.е. не зависит от деталей распределения и корреляционных свойств исходного шума (лишь бы функция корреляции убывала достаточно быстро).

Рассмотрим несколько компьютерных иллюстраций указанного свойства скейлинга. Начнем с серии графиков, каждый из которых изображает "зашумленный" аттрактор на итерационной диаграмме отображения окружности в координатах x(nF_k), x((n+1)F_k, где F_k - число Фибоначчи для k=6, 7, 8. При этом от картинки к картинке параметр шума уменьшается в g раз. Значения K и r отвечают критической точке GM. На каждой диаграмме выделен фрагмент вблизи начала координат, показанный отдельно с увеличением в a раз больше для каждой следующей картинки. Подобие объектов на этих увеличенных фрагментах иллюстрирует свойство скейлинга в системе с шумом.

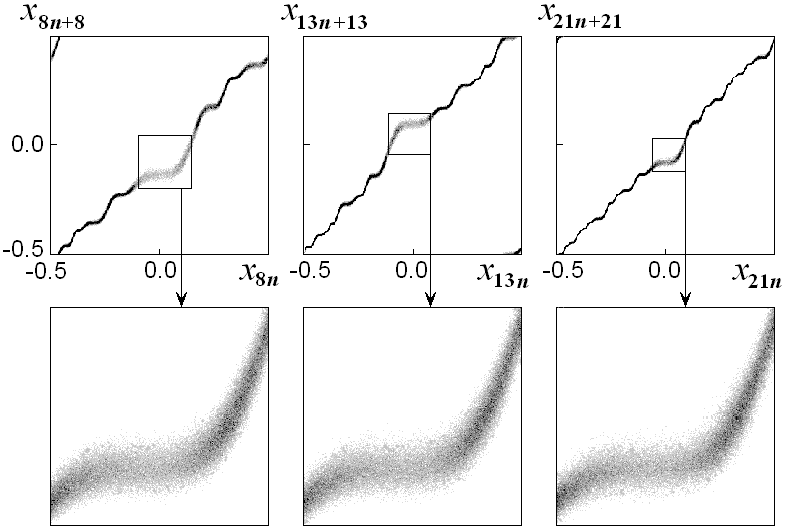
Обратимся теперь к диаграммам, показывающим зависимость числа вращения

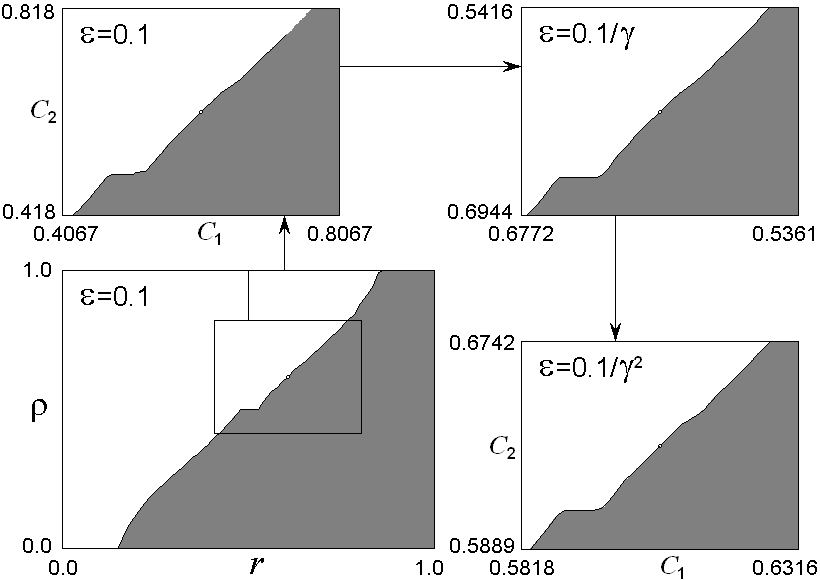
от параметра r при K=1. На основном рисунке и первой вставке приводятся разультаты расчета числа вращения при компьютерном моделировании динамики отображения окружности с шумом для e=0.1. Следующие картинки показывают фрагменты с возрастающим увеличением по горизонтальной и вертикальной оси, соответственно, на факторы d₁ и W². При этом каждый раз параметр шума уменьшается на фактор g. Обратите внимание на очевидное подобие графиков, представленных на малых диаграммах.

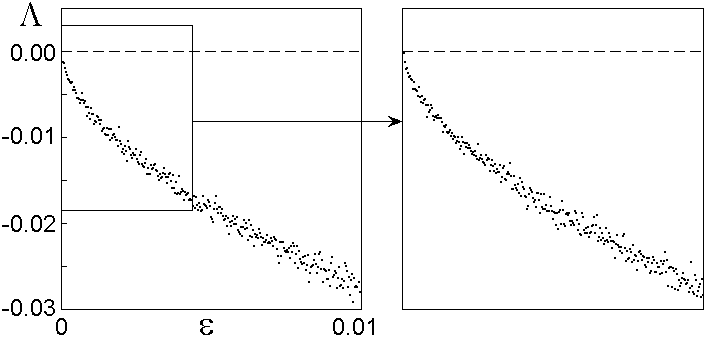
Следующая иллюстрация изображает зависимость показателя Ляпунова от интенсивности шума при значениях K и r, отвечающих критической точке GM. Из рисунак видно, что включение шума приводит к уменьшению показателя Ляпунова, т.е. способствует стабилизации (в противоположность тому, что имеет место для перехода по Фейгенбауму, когда присутствие шума способствует увеличению показателя Ляпунова). На вставке показан фрагмент графика с пересчетом масштаба по горизонтали на фактор g, а по вертикали - в W=(5^1/2-1)/2 раз. Сходство обеих картинок служит проявлением ожидаемого свойства скейлинга.

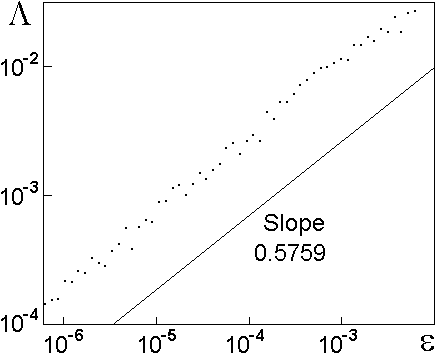
Другой способ продемонстрировать свойство скейлинга состоит в том, чтобы представить показатель Ляпунова в зависимости от уровня шума в двойном логарифмическом масштабе. Из графика видно, что точки располагаются в среднем вдоль наклонной прямой с угловым коэффициентом log_gW=0.5759, где W=(5^1/2+1)/2.

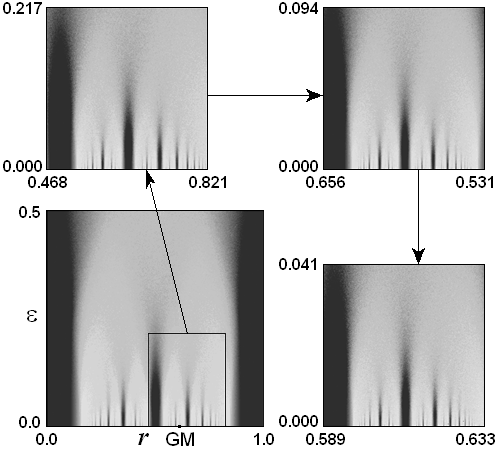
Следующая серия иллюстраций - ляпуновские карты, относящиеся к критическому значению параметра K=1. По горизонтальной оси отложен параметр r, а по вертикальной - параметр интенсивности шума e. Тона серого цвета от темных к светлым кодируют уровень показателя Ляпунова от минус бесконечности до нуля, а черный цвет соответствует положительным значениям показателя. При переходе к каждой последующей картинке для иллюстрации скейлинга масштаб по горизонтали и вертикали пересчитывается на факторы, соответственно, d₁ и g. Кроме того, переопределяется правило кодирования величины показателя Ляпунова серыми тонами с тем, чтобы учесть изменение характерного временного масштаба динамики на фактор W=(5^1/2+1)/2.

Наконец, последняя серия диаграмм - это ляпуновские карты, иллюстрирующие скейлинг картины языков Арнольда. Для этой демонстрации приходится ввести специальные локальные координаты (C₁,C₂) на плоскости параметров вблизи критической точки GM: одна координатная ось направлена вдоль критической линии K=1, а вторая - по линии постоянного числа вращения в отсутствие шума.

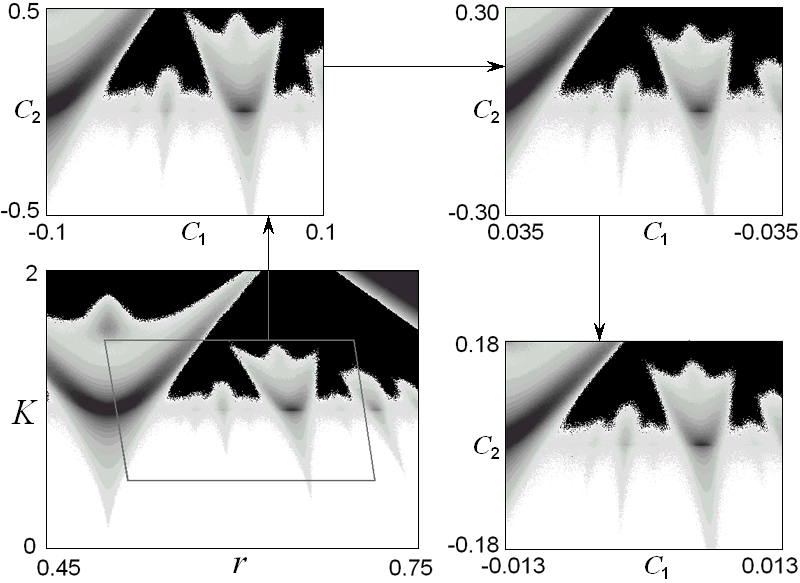
На основной диаграмме приведена ляпуновская карта на плоскости параметров отображения окружности (r,K) при уровне шума e=0.03. Первая вставка показывает внутреннюю часть выделенного параллелограмма в скейлинговых координатах, которые связаны с исходными параметрами модели соотношениями

Следующим двум картинкам отвечает параметр шума уменьшенный, соответственно, в g и g² раз. При этом масштабы по горизонтали и вертикали пересчитывается при переходе от одной картинки к следующей на факторы d₁ и d₂, и переопределяется надлежащим образом правило кодирования величины показателя Ляпунова тонами серого цвета.

• Действие шума на фейгенбаумовский тип поведения
• Действие шума при переходе к хаосу через квазипериодический режим с отношением частот "золотое среднее"
• Действие шума на критическое поведение, связанное с утроениями периода
• Влияние шума на критическое поведение модели с квазипериодическим воздействием в точке окончания линии бифуркации удвоения тора