на критическое поведение,
связанное с утроениями периода
 |
Действие шума на критическое поведение, связанное с утроениями периода |
Если в квадратичном отображении
zn+1=l-zn2
считать комплексными динамическую переменную и параметр,
то наряду с каскадом бифуркаций удвоения периода (при изменении
l вдоль действительной оси),
возможны также бифуркационные каскады утроения периода и другие.
 Гольберг, Синай и Ханин развили РГ анализ, аналогичный теории Фейгенбаума,
для последовательности бифуркаций утроения периода.
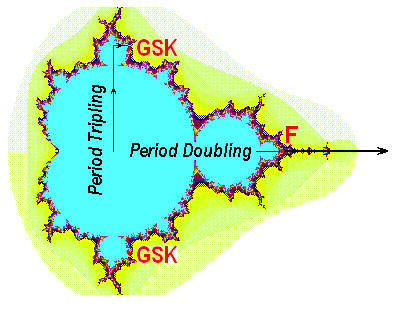
Справа на рисунке показана карта на плоскости комплексного параметра
квадратичного отображения, где имеет место фрактальное множество множество Мандельброта.
Оно образовано точками на плоскости параметра, которым отвечает динамика итераций отображения
при старте из начала координат в ограниченной области z.
На диаграмме отмечены критическая точка Фейгенбаума F на действительной оси и критическая точка
Гольберга – Синая – Ханина GSK, в которую можно попасть, двигаясь
по маршруту проходящему через «лепестки» множества Мандельброта
утраивающегося периода. В верхней полуплоскости точка GSK располагается при
Гольберг, Синай и Ханин развили РГ анализ, аналогичный теории Фейгенбаума,
для последовательности бифуркаций утроения периода.
Справа на рисунке показана карта на плоскости комплексного параметра
квадратичного отображения, где имеет место фрактальное множество множество Мандельброта.
Оно образовано точками на плоскости параметра, которым отвечает динамика итераций отображения
при старте из начала координат в ограниченной области z.
На диаграмме отмечены критическая точка Фейгенбаума F на действительной оси и критическая точка
Гольберга – Синая – Ханина GSK, в которую можно попасть, двигаясь
по маршруту проходящему через «лепестки» множества Мандельброта
утраивающегося периода. В верхней полуплоскости точка GSK располагается при
lGSK = 0.0236411685 + 0.7836606508i,
а в нижней – при сопряженном значении l. [А.И.Гольберг, Я.Г.Синай, К.М.Ханин. Универсальные свойства последовательности утроения периода. УМН, 38, №1, 1983, 159-160.]
Вблизи критической точки GSK структура "лепестков" множества Мандельброта
обладает свойством масштабной
инвариантности относительно пересчета
Рассмотрим теперь стохастическое отображение
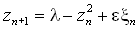
где xn - последовательность статистически независимых комплексных случайных величин с нулевым средним и фиксированным среднеквадратичным значением s. Как видно из следующего рисунка (построенного для e=0.001), в присутствии шума масштабная инвариантность ляпуновской карты нарушается.
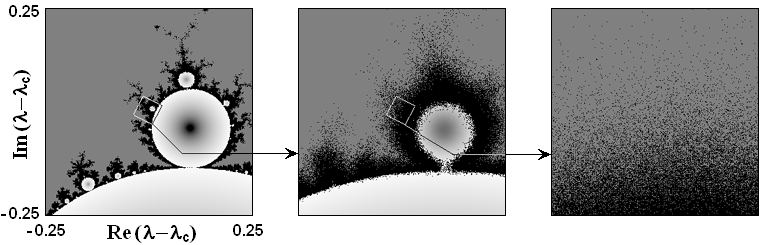
Ренормгрупповой (РГ) анализ задачи с шумом приводит к заключению, что существует универсальная константа, которая показывает, во сколько раз надо уменьшить амплитуду воздействующего на систему шума для того, чтобы можно было наблюдать каждый новый уровень утроения периода: g=12.2066409 [Isaeva, Kuznetsov, Osbaldestin, 2004] (Содержание РГ анализа изложено здесь.)
Предположим, что при каком-то значении комплексного параметра l
близком к критической точке GSK и при достаточно малом уровне шума
e наблюдается некоторый режим поведения модели. Тогда при
отклонении от критической точки по параметру
(l-lGSK)/d,
где
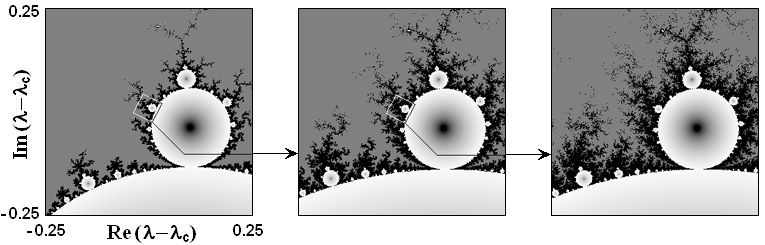
Рассмотрим две компьютерные иллюстрации указанного свойства скейлинга.
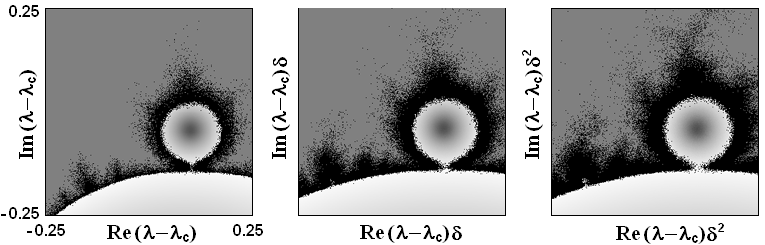
На первом рисунке показаны карты показателя Ляпунова, аналогичные предыдущей диаграмме, но, в отличие от нее, на каждому очередному рисунку отвечает уровень шума, уменьшенный на фактор g. Видно, что подобие картинок восстанавливается.
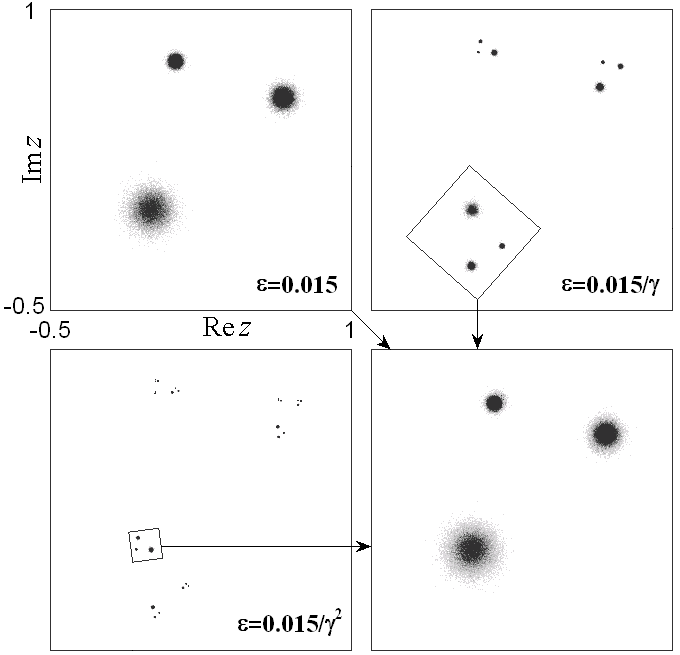
На следующем рисунке представлены портреты "зашумленных аттракторов" комплексного квадратичного отображения при значениях параметра, отвечающих в системе без шума так называемым сверхустойчивым циклам периода 3, 9 и 27, т.е. имеющим в своей орбите точку z=0, что имеет место при
и для значений амплитуды шума, подписанных на графиках. Как можно видеть, при надлежащем пересчете комплексной координаты (см. выделенные фрагменты на диаграммах), вид портрета аттрактора выглядит примерно одинаково.