Интересно сравнить динамику квантового вектора состояния для систем, отвечающих отображениям на торе гиперболического, параболического и эллиптического типа (см. таблицу).

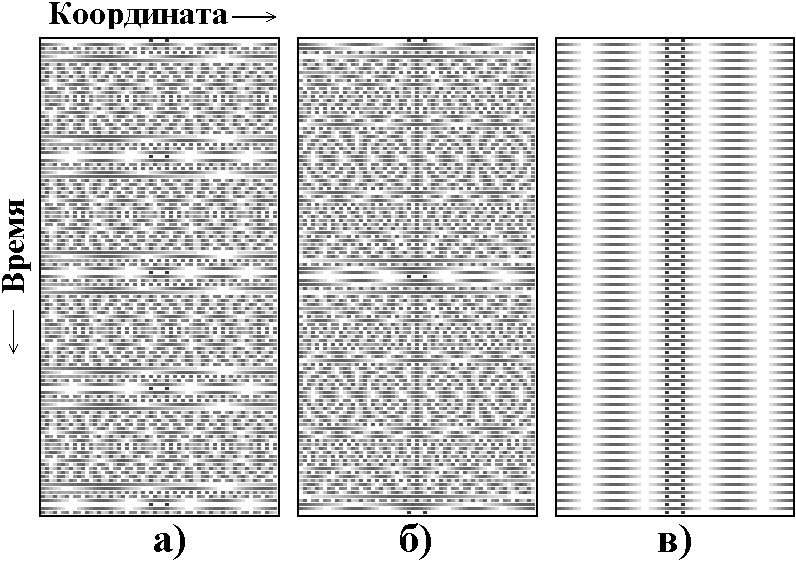
Приведенный ниже рисунок иллюстрирует эволюцию волнового пакета в системе гиперболического (а), параболического (б) и эллиптического (в) типа при N=59. В начальный момент пакет имеет вид y_mµexp(-pm²/N+2piPm/N) и характеризуется минимальной шириной, допускаемой принципом неопределенности. Начальный сдвиг по импульсу P=3.

Обратим внимание, что эволюция во времени во всех случаях периодическая. С точки зрения пространственного распределения волновых функций, никакого хаоса не видно даже в гиперболическом случае. Для отображений всех трех классов более характерным кажется как раз наличие в каждый момент вдоль пространственной оси достаточно регулярного набора чередующихся интерференционных максимумов и минимумов.

Для гиперболического отображения эволюция волнового пакета сопровождается быстрым расширением на первых же шагах дискретного времени. После этого распределение амплитуды по длине системы становится более или менее однородным, хотя встречаются моменты, когда отклонение от однородности значительное, и распределение концентрируется в нескольких узких интервалах.

Для параболического отображения расплывание происходит гораздо медленнее. Когда характерная ширина пакета становится сравнимой с длиной системы, на краях появляются темные и светлые интерференционные полосы. В дальнейшем эта интерференционная картина покрывает всю систему, изменяясь во времени сравнительно медленно и регулярным образом.

Для эллиптического отображения волновой пакет не расплывается и просто совершает колебания с периодом в четыре итерации.

Как было показано, операторы сдвига по координате и импульсу в представлении Гейзенберга выражаются через две пары определенных по модулю N целочисленных переменных, (s,q) и (r,p), и каждая пара подчиняется уравнениям, совпадающим по виду с исходным классическим отображением. Переменная q существенна с точки зрения структуры вектора состояния в координатном представлении: волновая функция становится "разреженной", если q имеет с квантовым параметром N общий делитель. Таким образом, с точки зрения квантовой динамики на торе, важна структура разложения N на простые множители.

В случае параболического отображения эта структура полностью "раскрывается" в процессе динамики, поскольку переменная q пробегает в течение квантового периода все целочисленные значения от 0 до N-1. Доля моментов времени, когда волновая функция разрежена, дается отношением f(N)/N, где f(N) - функция Эйлера (количество натуральных чисел от 1 до N-1, являющихся взаимно простыми с N).

Для эллиптического отображения упомянутая арифметическая структура N несущественна, поскольку q оказывается попеременно нулем или числом взаимно простым с N. Волновая функция осциллирует между двумя возможными ситуациями - полной локализации и полной делокализации.

Для гиперболического отображения кота Арнольда переменная q в течение квантового периода посещает лишь часть возможных значений, и при этом не проявляет видимой регулярности. Соответственно, в пределах квантового периода ситуации прореживания и полной делокализации волновой функции чередуются хаотически. Арифметическая структура N существенна, но ее проявление замаскировано.

Если N простое, картина выглядит наименее содержательной: чаще всего волновая функция полностью делокализована (амплитуда равномерно распределена по координате) и лишь один или два раза за период наступает локализация в одной точке.

На рисунке приводятся диаграммы, иллюстрирующие квантовую динамику состояния исходно локализованного в начале координат: (а) отображение кот Арнольда, N=59, (б) отображение кот Арнольда, N=63, (в) отображение параболического типа, N=63.

В учебниках квантовой механики почетное место занимает описание опыта с интерференцией от двух щелей. Для квантовых отображений на торе аналогом этого опыта служит задача об эволюции в дискретном времени волновой функции, имевшей в начальный момент вид двух дельта-пиков, разнесенных по координате на некоторое расстояние. На следующих шагах дискретного времени суперпозиция волновых функций, порожденных этими двумя источниками, образует некоторую одномерную интерференционную картину, изменяющуюся от шага к шагу. Если один дельта-пик находился в начальный момент на позиции l₁, а второй - на позиции l₂, то волновая функция будет определяться линейной комбинацией двух составляющих, задаваемых соотношениями вида.

Обсудим случай простых N. Тогда для любого целого q от 1 до N-1 можно найти лежащее в этих же пределах число Q, являющееся обратным по модулю N, т.е. такое, что qQ=1 (mod N). Согласно малой теореме Ферма, Q=q^N-2 (mod N).

Суперпозиция составляющих, порождаемых двумя начальными дельта-пиками имеет вид

Отсюда видно, что комбинация Q|l₁-l₂| играет роль волнового числа пространственной интерференционной картины.

Для параболического отображения q пробегает за период все числа от 1 до N-1. Соответственно, те же значения, но в другом порядке, пробегает величина Q. Динамика как бы разворачивает перед нами присущую числу N арифметическую структуру, закодированную в порядке появления различных чисел среди обратных к последовательным целым.

Напротив, динамика отображения эллиптического типа совсем не несет информации об этой структуре: каким бы ни было число N, величина q пробегает всегда одни и те же значения 0, -1, 0, 1.

В гиперболическом случае на временах меньших периода возврата последовательность q носит хаотический характер. Соответственно, обратное число, Q также беспорядочно блуждает по своему множеству значений, тем самым маскируя упомянутую арифметическую структуру N.

Итак, взаимосвязь между квантовой эволюцией и классической динамикой проявляется в том, как изменяется во времени пространственный период интерференционной картины. Для отображения кота Арнольда это изменение на конечном интервале времени, в пределах одного полупериода, выглядит нерегулярным, хаотическим. Для отображения параболического типа оно более плавное и регулярное. Для отображения эллиптического типа распределение в виде двух дельта-пиков повторяется на каждом втором шаге итераций, а на промежуточных шагах имеет место интерференционная картина с одним и тем же пространственным периодом.