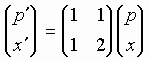
Let a particle of mass m can move freely on the circle of length L_x, and its coordinate x is the length of arc along the circle. The motion takes place in presence of external field that is switched on periodically, as short pulses, with time period T. Distribution of the field in x is assumed of such kind that The momentum accepted by the particle is proportional to the coordinate at the moment of the pulse: p=gx. Beside, we assume that the phase space also is periodic in respect to momentum, with period L_p, i.e. the momentum values separated by L_p, are equivalent.

Remark. The last assumption is not so artificial as one could think. Say, in solid state physics, for quantum excitations (quasiparticles) the notion of quasimomentum is used instead the ordinary momentum, and the periodicity in respect to the quasimomentum takes place with a period inversely proportional to spatial period of the crystal lattice.

If the particle has position and momentum p and x at the moment before the n-th kick, then, just after the kick the position remains yet the same, but the momentum becomes equal to p'=p+gx. Then, the particle moves by inertia with velocity p'/m. After time interval T the increase of the coordinate will be Dx=p'T/m, and before the next kick we have

p'=p+gx (mod L_p),
x'=x+p'T/m (mod L_x),

where the mod sign reminds that the position and momentum are defined up to integer number of periods L_x or L_p. Selecting the parameters in such way that gL_x/L_p=1 and gT/m=1, and normalizing the momentum and coordinate by factors L_p and L_x, we obtain

p'=p+x, x'=x+p' (mod 1),

or

p'=p+x, x'=p+2x (mod 1).

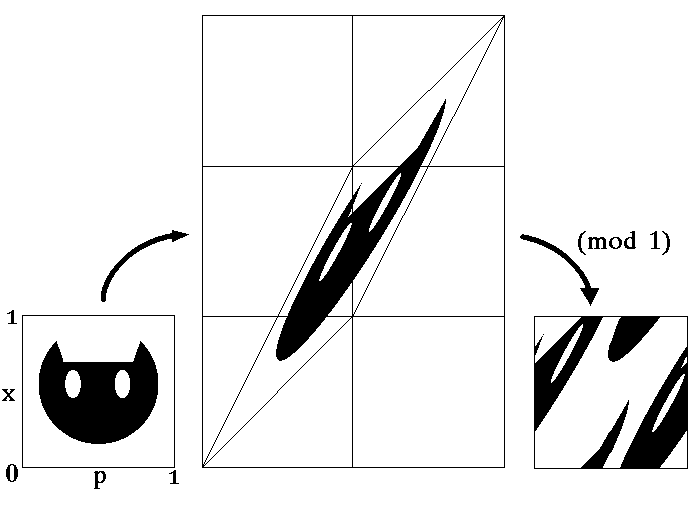
The constructed mapping of variables p and x is called Arnold's cat map. This name is due to V.I.Arnold who explained the action of this map using the picture of the cat face (see figure). Geometrically, the first step of the procedure consists in linear transformation of the variables

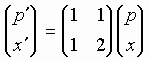
and the second one in transfer of elements of the picture again inside of the unit square (the mod operation). Due to periodicity in x and p, the phase space may be regarded as the surface of a torus. The particle motion is conservative, i.e. we deal with a Hamiltonian system. Mathematically, it is connected with the fact that the determinant for the matrix associated with the Arnold cat map equals 1, and it conserves the measure (area) of any domain, say, of the cat face. In terms of classic mechanics, this is the canonical transformation.

One can consider more wide class of maps on the torus, which are determined by integer element matrices

,

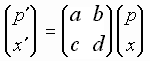satisfying the condition ab-cd=1. In dependence on the eigenvalues l₁, l₂, the maps of such kind relate to one of the three types:

hyperbolic, if one eigelvalue is larger than 1, and the second is less than 1,

parabolic, if l₁=l₂=1,

ellipic, if l₁ and l₂ are complex conjugate.

The Arnold cat map is of the hyperbolic type as the eigenvalues are l₁=(3+5^1/2)/2 and l₂=(3-5^1/2)/2. The values L₁=logl₁ and L₂=logl₂ are the Lyapunov exponents, one of which is positive. This is the known sign of presence of sensitivity of motion to variation of initial conditions, the important attribute of the dynamical chaos.

If we exclude the pulses of external field in the above consideration, the result will be a parabolic type map describing free motion of the particle:

p'=p, x'=p+x (mod 1).

Canonical transformation swapping position and momentum is an example of an elliptic map:

p'=x, x'=-p (mod 1),

In the figure we show evolution of some initial area under subsequent iterations of the maps of hyperbolic (�), parabolic (b) and elliptic (c) type.

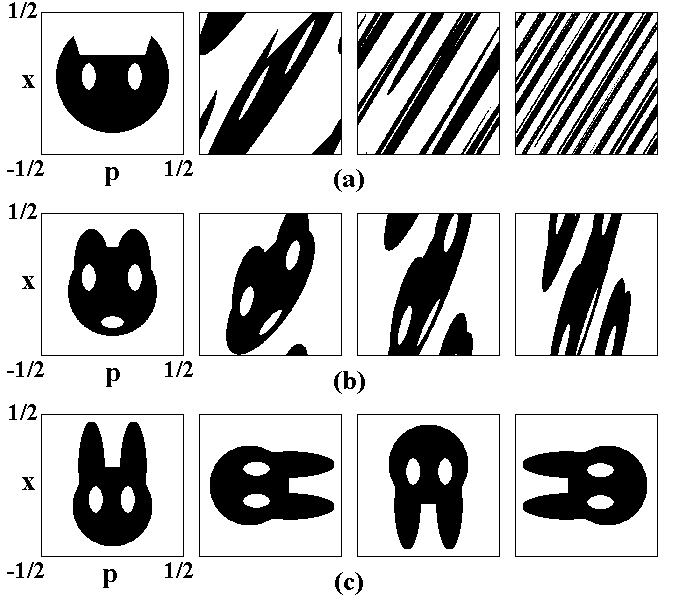
In the parabolic case the image of the figure remains in the definite initial interval of momentum. In the elliptic case the evolution consists in rotation without other changes of the form.

Under iterations of the hyperbolic map the cat face is stretched along the unstable eigenvector, at each step by the factor l₁ and compressed along the second (stable) eigenvector by the factor l₂. After a large number of iterations the cat face transforms into an extremely narrow strip stretched along the unstable direction, that is close to a long segment of straight line p=kx, k=(5^1/2-1)/2. As the coefficient is irrational, this line covers the torus surface dense everywhere. So, the picture looks like a set of a large number of the narrow black and white strips, which arise from the cat face and its complimentary set, respectively. In the usual language, we should say that the "black" and "white" liquids are well mixed. The mixing property may be formulated mathematically. Presence of mixing is proved rigorously for the hyperbolic maps and serves as a basis for a conclusion on the chaotic nature of the dynamics.

Comparing figs (a)-(c), one can see that neither parabolic, nor elliptic maps manifest the mixing property.