In a quantum system with constant parameters and dynamics in bounded region the Schrodinger equation gives rise to a discrete spectrum of eigenvalues, the allowed energy levels. In systems with periodic variation of parameters in time, and in discrete time systems, instead of the energy spectrum people introduce the spectrum of quasienergies. Let the evolution of state vector over a period t is governed by a unitary operator U. Let us formulate the eigenproblem: U|ys>=ls|ys>. As the operator is unitary, its eigenvalues are equal to 1 in modulus, and we set ls=exp(2piEs/h). The value Еs is quasienergy of an eigenstate. |ys>. It is defined up to a constant shift h/t.
For maps, t is one step of discrete time. As the evolution operator for quantum map on torus is represented by a matrix NxN, the spectrum must contain N eigenvalues ls=exp(iqs), among them there may be the degenerate ones. The values qs, which just play role of the quasienergies are called also the eigenangles. A vector |ys> will be an eigenvector of the operator Uk, with the eigenvalue (ls)k. Existence of the quantum period T(N) implies that UT(N)=1. Hence, (ls)T(N)=1, and all eigenvalues ls must be the complex roots of 1 of power T(N), i.e. to belong to a set {1, w, w2,..., w T(N)-1 ), where w=exp[2pi/T(N)]. The only question is: Which roots from this set are present in the spectrum, and how many times (what are the numbers of degeneracy?).
The trace of the matrix Tr(U) is equal to the sum of all the eigenvalues, and for the matrix Uk it is a sum of their k-th powers:
The "trace-последовательность" Sk has the period T(N) and allows the representation via the Fourier series:
![]()
It is seen that the coefficient at the r-th term of the expansion
![]()
is a number of degeneracy for the eigenvalue wr in the spectrum of the evolution operator. As follows, to obtain the spectrum of the evolution operator it is sufficient to take the trace sequence and produce the discrete Fourier transform. The very straightforward way is to compute subsequent powers of the matrix Uk, and sums of diagonal elements Sk. (In fact, much more effective algorithms may be designed.) In figures below we show diagrams presenting the trace-sequences and quasienergy (eigenangle) spectra for the Arnold cat map at some numbers N.
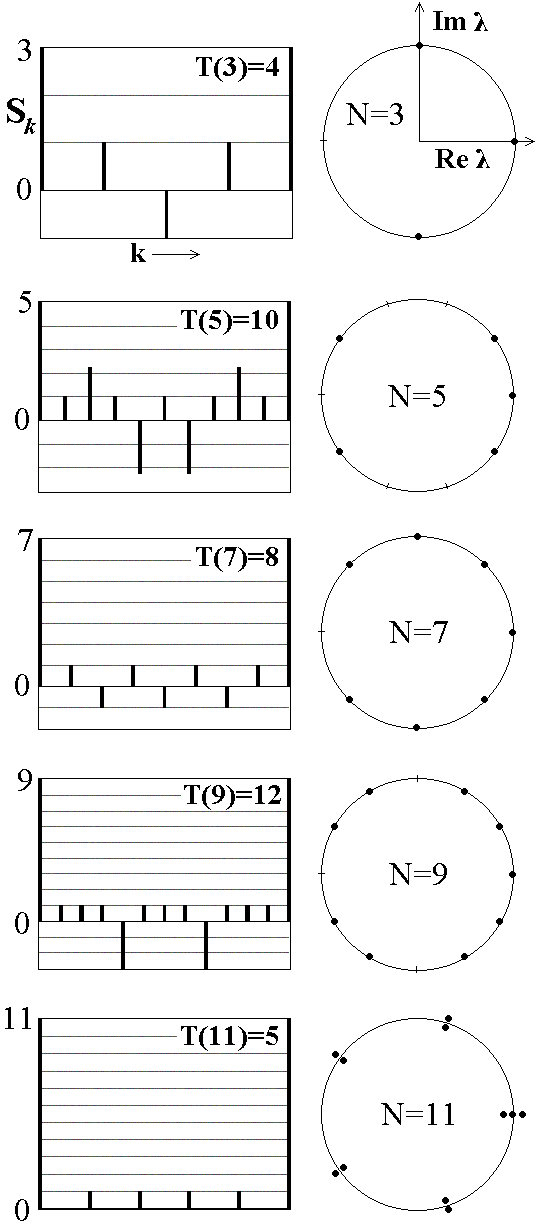
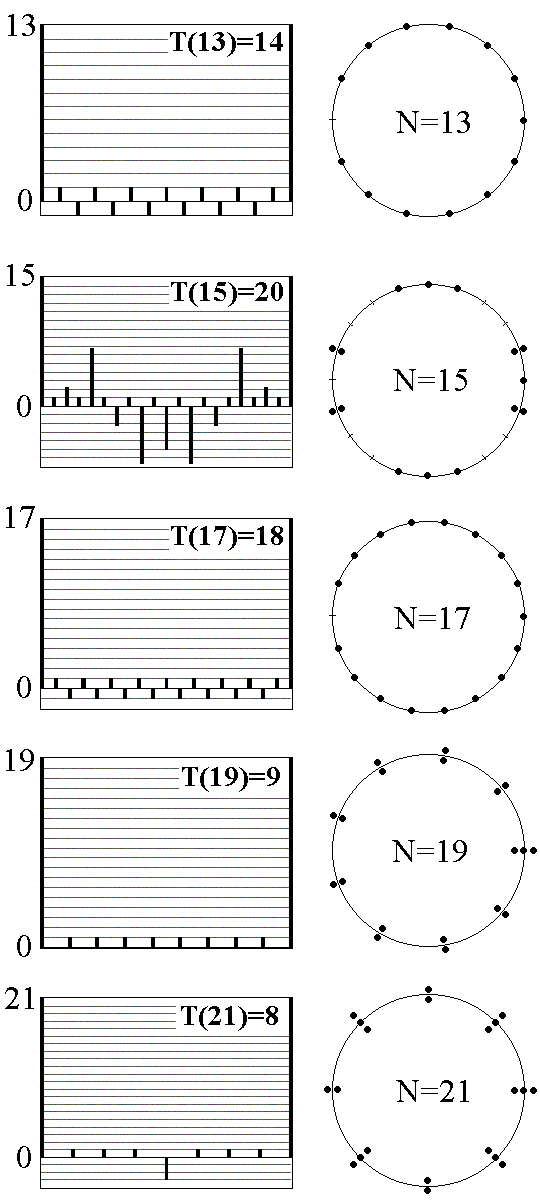
The next figure presents comparison of the dependencies of quasienergies on the quantum parameter N for the maps of hyperbolic (a), parabolic (b), and elliptic (c) type.
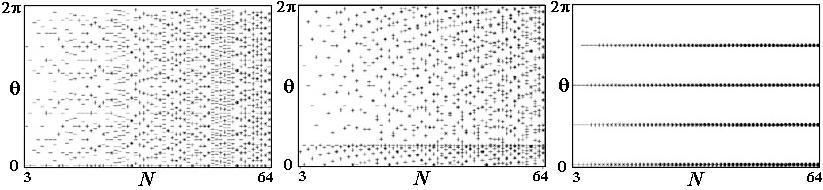
In the distribution of the levels of quasienergy of maps with regular dynamics one can distinguish ordered structures, but in the Arnold cat map ("chaos") such structures are obviously not visible.
The next interesting question: Can we see any difference in the structure of eigenvectors in the quantum maps with regular and chaotic dynamics of classic analogs? Let us take some probe vector |y0> and, acting with the evolution operator U step by step construct the sequence |yk>=Uk|y0>. Due to the existence of the return period, this sequence may be represented by the Fourier series:
![]()
As "coefficients" in this expression we have the (non-normalized) eigenvectors of the evolution operator. A vector
![]()
corresponds to the eigenvalue ls=exp(2pis). If the number exp(2pis) is absent in the spectrum at some s, then the respective term of the sum is zero.
The figure below shows spatial distributions and Husimi distributions for several eigenvectors of the quantum Arnold cat map at N=131. For comparison the next two pictures show examples of eigenvectors for the parabolic and elliptic maps (regular dynamics in classic analogs).
Arnold's cat map
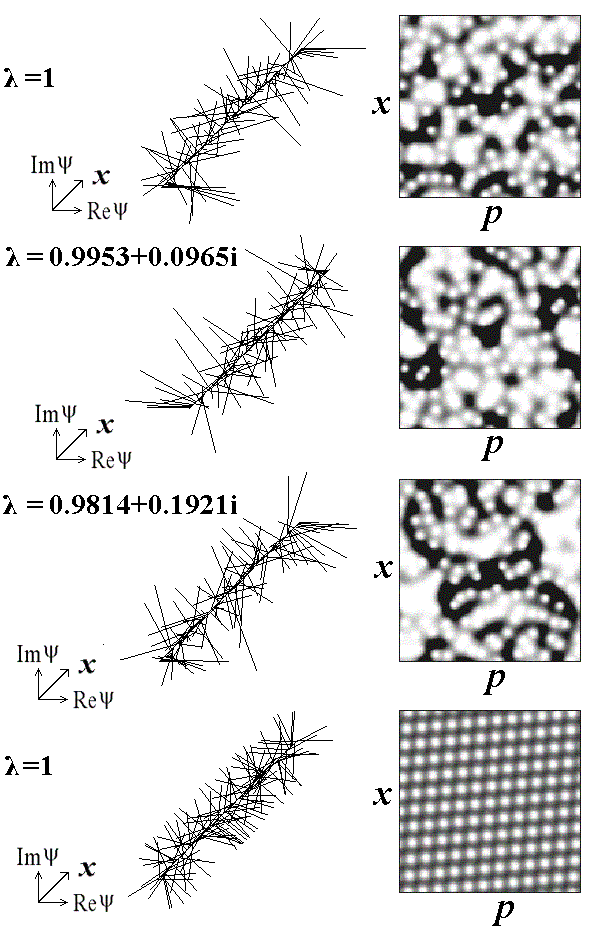
Parabolic map
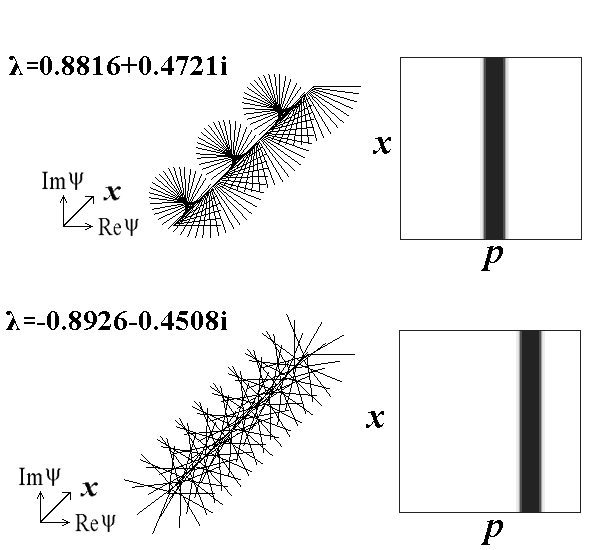
Elliptic map
