
In classic dynamics and chaos theory we use a concept of phase space. Time evolution of an individual system corresponds to a motion of the representative point along the phase trajectory (orbit). Dynamics of an ensemble (a collective of independent identical systems distinct only with the initial conditions) may be thought as evolution of a cloud of representative points in the phase space and the density function is the distribution function governed by the Liouville equation.
Due to the uncertainty principle, in the quantum theory the ordinary distribution function cannot be defined f(p,x), because we cannot construct the ensemble of systems possessing simultaneously by a certain momentum p and a position x.
One possibility to introduce a quantum analog of the distribution function is to use the so-called Husimi distribution, and another is based on the Wigner function.
Husimi distribution
For a quantum system the phase plane may be thought as a collection of cells of size DpDx=h/2p, and we speak on a probability of presence at each cell. To define it one can estimate an overlap integral of the wave function |y> with a coherent state |ypx>, centered at the given point (p,x). The function of two variables fH(p,x)=|<ypx|y>|2 constructed in this way is called the Husimi distribution. In the classic limit, as h goes to zero, the coherent state turns into the delta-function, and the Husimi distribution tends to the ordinary distribution function.
Remark: What is the coherent state? Following Glauber, the coherent state |y0> centered at the origin is defined as an eigenvector of the operator a=(x+ip)/21/2 with zero eigenvalue. The equation in position representation has a form xy+(h/2p)dy/dx=0, and the solution is yµexp(-x2/2ph). Then, we construct states shifted in momentum and coordinate by arbitrary values p and q: |ypq=exp((p+iq)a)|y0. For the maps on torus an appropriate generalization suggested by Saraceno is based on a difference analog of the operator a. The state centered at the origin is defined by an equation (A-A++i(K-K+))|y0>=0. States shifted in momentum and position by p and q positions, respectively, may be obtained by application of the operator K+qAp.
The figure below shows evolution of the Husimi function in the quantum Arnold cat map at N=131. The initial state is the Gaussian packet of maximal localization. Gray tones code levels of the function fH(p,x). The initial stage of the evolution of the Gaussian packet demonstrates evident similarity with the pictures of the cat face transformations in the classic case. When the width of the packet becomes larger than the spatial period, the interference pattern appears as a result of superposition of the "tails" transferred into the unit square from other parts of the picture.

Wigner function
For one-dimensional motion of the quantum particle the Wigner function is expressed via the wave function as y
(x): 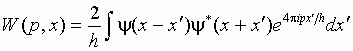
The value W(p,x) is always real.
Wigner function is used widely in statistical physics in the quantum consideration instead of the ordinary distribution function in classic statistics. The reason is that integration of the Wigner function over the firs argument yields the probability distribution for coordinate, and integration over the second argument to the distribution for momentum:
![]()
Under the periodicity conditions on the torus the Wigner function W looks like a set of delta-peaks at nodes of square lattice with step 1/2N in the unit square. It is defined by a table of 2Nx2N real numbers associated with the amplitudes of the delta-peaks:
![]()
where k and m accept integer and semi-integer values (0, 1/2, 1, 3/2,...N-1/2).
Summation of w(k,m) over k yields the probability distribution for coordinate, and summation over m - the probability distribution for momentum:
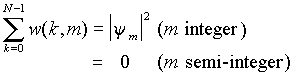
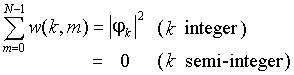
It may be shown that evolution of the Wigner function for the Arnold cat map is governed by a simple expression
![]()
In other words, the values of the Wigner function associated with the nodes of the lattice 2Nx2N simply transfer along the classic orbits on the lattice:
![]()
Remark. The additional term 1/2 in the equation for k', is in a sense irrelevant, it can be excluded by a shift of origin m->m-1/2, k->k+1/2. This redefinition is not so convenient because forces us to deal with the semi-integer indices, although recover exact correspondence with the classic map.
In the figure below we show evolution of the Wigner function in the Arnold cat map at N=13. The initial state is the Gaussian packet. The evolution is periodic: return to the original state occurs after 14 steps. A peculiar feature of a hyperbolic map is that the essentially non-zero values of the function at intermediate steps are dispersed more or less uniformly over the unit square.
