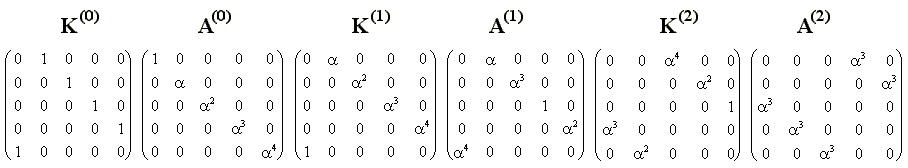
In quantum mechanics, each physical variable ("observable") is associated with a Hermitian operator. In Heisenberg representation, the operators evolve in time, while the state vector does not depend on time. In our case, the operatirs act in the vector space of dimension N and are represented by matrices of size NxN.

Let us start with a trivial remark that the classic Arnold cat map may be reformulated avoiding the modulus operation. To do this we introduce new variables K=exp(2pip) and A=exp(2pix), instead of p and x. Then, the map p'=p+x, x'=p'+x=p+2x will be rewritten as K'=KA, A'=AK'.

Accounting the remark, it is worth formulating the Heisenberg representation of the dynamics in terms of the operators associated with the variables K and A. These are the operators of finite shift for position and momentum, known as the Weyl-Heisenberg operators.

Indeed, let us consider the operator K_a=exp((2pi/h)ap), where p=-(ih/2p)d/dx is the momentum operator, a is an arbitrary real number. If we write out the Taylor expansion for this operator it becomes evident that it coincides with the finite shift operator by the distance a:

K_ay(x)= exp((2pi/h)ap)y(x) +ay'(x) +(1/2)a²y''(x) +(1/6)a³y'''(x)+... = y(x+a).

In the momentum representation action of the operator K_a corresponds simply to multiplication by K_a(p)=exp((2pi/h)ap)j(p).

The operator of the momentum shift by b in the position representation is defined as multiplication by factor A_b(x)=exp((2pi/h)bx)y(x). In the momentum representation this is the operator A_b(p)=exp((2pi/h)bx)j(p) where x=(ih/2p)d/dp.

The result of action of operators K_a and A_b onto function y(x) depends on their order:

K_aA_by =exp((2pi/h)(bx+ba))y(x+a),
A_bK_ay =exp((2pi/h)bx)y(x+a).

This may be written in a form of the commutative relation K_aA_b=exp((2pi/h)ba)A_bK_a, which replaces the known position-momentum relation px-xp=-ih/2p.

As mentioned, the wave function of unit periods for coordinate and momentum is a comb of delta-functions with step of 1/N both in the position and momentum representations. Let us define the shift operators taking 1/N as the shift constant and setting h=1/N:

Then, the commutation relation becomes

KA =aAK, a=exp(2pi/N).

Now we have all necessary to construct the quantum analog of the Arnold cat map in terms of operators K and A. We simply change K and A with the respective operators and obtain the operator map

K'=KA, A'=AK'

or

K'=KA, A'=AKA.

So, the operators K' and A' corresponding to the next time step are expressed via the operators defined at the previous step. To interpret them again as the shift operators it is necessary to have the same commutation relation. As may be checked easily, this is indeed true:

K'A'=(KA)(AKA)=a(AKA)(KA)=aA'K'.

As the state vector is represented by a set of N coefficients y_m, the operators K and A must be represented my matrices of size NxN, and it is natural to define them as follows:

(Ky)_m=y_m+1, (Ay)_m=a^my_m.

It corresponds to the matrices

K_mn=d_m+1,n and A_mn=a^md_mn; m, n =0, 1, 2, ... N-1,

where d_mn=1, if m=n (mod N), else d_mn=0.

As it will be clear in the next section, the quantization schema based on the above relations is appropriate for odd N only .

(Generalization for even N see here.)

In the Heisenberg representation the state vector does not depend on time, which is the iteration number, while the operators associated with the dynamical variables, vary at each iteration. Setting initial conditions for the operator map with the matrices K⁽⁰⁾=K and A⁽⁰⁾=A, we obtain recursively the matrices K^(k) and A^(k) for subsequent time steps k. For example, for N=5,

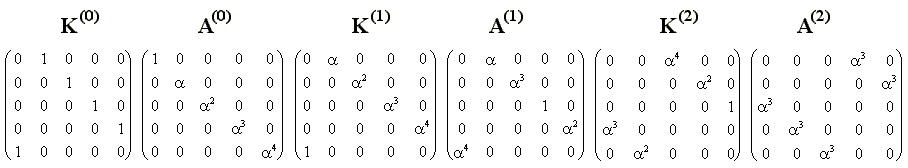
and so on. Each matrix in this sequence is a product of two previous ones.

It is evident from this example that each time nonzero elements are arranged along the line parallel to the main diagonal, i.e. the matrices are of the form
K^(k)_mn=d_m+s,na^nr+n, A^(k)_mn=d_m+q,na^np+m. Two pairs of integers, s and q, r and p, obey the equations of the same form as the classic Arnold cat map:

s'=s+q, q'=q+s', r'=r+p, p'=r+p' (mod N).

Two additional variables m and n obey equations, in which s, r, p, q play a role of external periodic force:

n'=n+m-rq, m'=n'+m-ps' (mod N).

The dynamics takes place on a finite set of integers, and, hence, is not chaotic, it is periodic.

The period T(N) of the operator sequence K, � in the Heisenberg representation is also a period of the wave funcnction evolution in the Schrodinger representation. For example, T(5)=10. The figure shows a plot of the quantum period T(N) for the Arnold cat map. Observe that the dependence is extremely irregular, although in average the period grows with N.

Remark I. As the operators K and A do not commute, our selection of the operator map is not unique. As well, we could define a map with rearranged operators K and A (say, K'=AK, A'=KAA or others). Although the commutation relation allows returning to the original disposition of operators, it leads to appearance of factor a in some power. The dynamics then is modified, but the quantum period remains unchanged.

Remark II relates to quantization of more general maps on torus. If a matrix is of a form

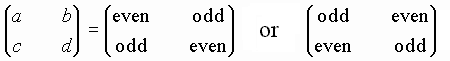
there exists a natural logical way to select the version of the operator map using the symmetrized combinations of K and A. In the first case the operator map may be chosen as K'=K^a/2A^bK^a/2, A'=A^d/2K^cA^d/2, and in the second as K'=A^a/2K^aA^b/2, A'=K^c/2A^dK^c/2. This class of maps was named as quantizable in the original work of Hannay and Berry. The Arnold cat map does not relate to this class. In fact, this does not mean that the quantization is impossible at all, but the consequence is that the basic relations for the quantum Arnold cat map are distinct for odd and even N.

Remark III.
Operator map of parabolic type describing free motion of the particle may be defined as K'=K, A'=AK.
Quantum analog of the elliptic map, the canonical transformation exchanging coordinate and momentum variables look as follows: K'=A, A'=K⁺, where cross means the Hermitian conjugate.