It is interesting to compare the dynamics of the quantum state vector for systems associated with maps on torus of hyperbolic, parabolic, and elliptic types (see Table).

The following figure illustrates evolution of a wave packet in a system of hyperbolic (a), parabolic (b), and elliptic type at N=59. Initially the packet is of minimal width allowed by the uncertainty principle: y_mµexp(-pm²/N+2piPm/N). The initial momentum shift is P=3.

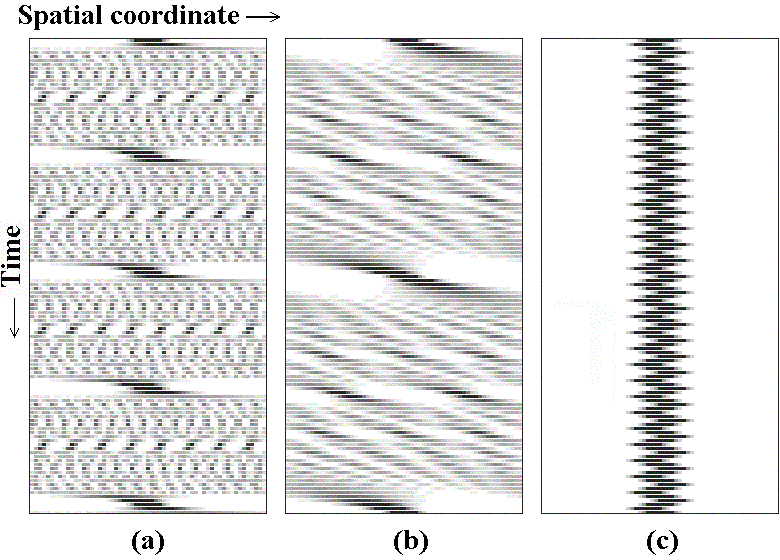
Note that the evolution in all three cases is periodic. From the point of view of spatial distribution of the wave functions, no chaos is observed even in the hyperbolic case. Moreover, rather regular spatial pictures of interference maxima and minima seem typical for all three classes.

For the hyperbolic map, the evolution is accompanied by rather fast increase of width at the first steps of discrete time. Then, the amplitude distribution over the length becomes more or less uniform, although at some moments the deflections from the uniformity are strong, and the distribution is concentrated at several narrow intervals.

For the parabolic map, the increase of width of the packet is much slower. As the characteristic width becomes comparable with the total system size, at the edges the dark and bright interference strips appear. Gradually this interference picture covers the whole length and evolves relatively slowly and regularly.

For the elliptic map, the wave packet does not increase the width but simply oscillates with a period of 4 iterations.

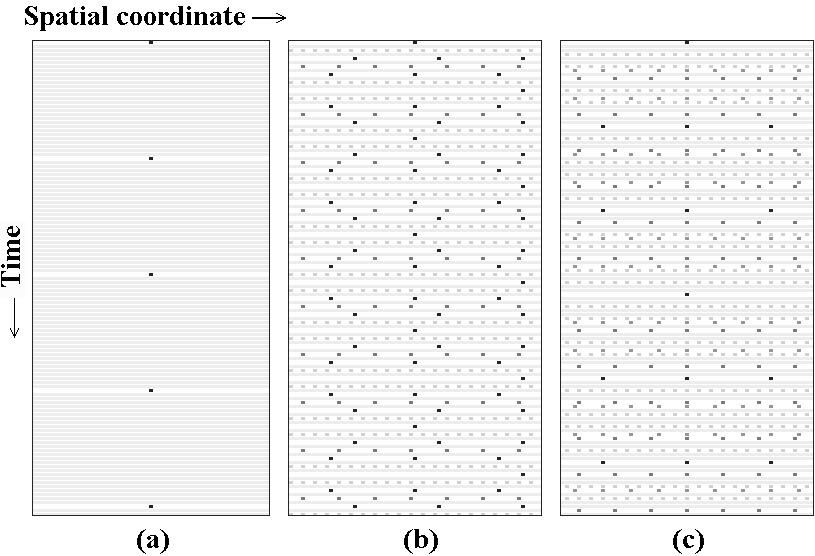
As shown, the operators of the position and momentum shifts in Heisenberg representation may be expressed via two pairs of integer variables defined modulo N, namely, (s,q) and (r,p), and each pair obeys equations, coinciding in a form with the classic map. The variable q is relevant for the structure of the state vector in the position representation: the wave function becomes "sparse" if q has a common divisor with the quantum parameter N. Thus, for the quantum dynamics on torus the structure of prime decomposition of N is important.

In parabolic map, this structure completely reveals itself in the process of dynamics, as the variable q runs over all integers from 0 to N-1 on a quantum period. A fraction of moments of time, when the wave function is sparse, us given by the ratio f(N)/N, where f(N) is the Euler function (number of integers from 1 to N-1 mutually prime with N).

In elliptic map, the mentioned number-theoretic structure of N is irrelevant, as q appears to be alternatively 0 and an integer mutually prime with N. The wave function oscillates between two states of full localization and full delocalization.

In the hyperbolic Arnold cat map, the variable q visits only a part of possible values, and do not show visible regularity. Accordingly, during the quantum period the situations of sparse structure and of full delocalization alternate chaotically. The number-theoretic structure of N is relevant, but its manifestation is in a sense masked.

If N is prime, the picture looks the most simple: almost always the wave function is fully delocalized (the amplitude is distributed uniformly), and only one or two times over the period the localization at one point occurs.

The diagrams show quantum dynamics of the state originally localized at the origin in the Arnold cat map ((a) - N=59 and (b) - N=63), and in the parabolic map ((c) - N=63).

In all textbooks in quantum mechanics the two-slit interference experiment is usually discussed in details. For the quantum maps on torus the analog of this experiment is the problem of the evolution of the wave function initially composed of two delta-peaks. On the next steps of the discrete time evolution, the superposition of the wave functions produced by this two sources forms some interference picture changed from step to step. Let the initial positions of the two delta-peaks be l₁ and l₂, respectively.

Let us discuss a case of prime N. Then, for any integer q from 1 to N-1 we can find in the same interval an integer Q that is inverse to q modulo N: qQ=1 (mod N). According to Fermat theorem, Q=q^N-2 (mod N).

The superposition of states produced by two initial delta-peaks is given by

Hence, the combination Q|l₁-l₂| plays a role of the wave number of the spatial interference picture.

For the parabolic map the variable q visits all integers from 1 to N-1. Respectively, the same values in other order the value Q accepts. To say, the dynamics step by step resolves the arithmetical structure intrinsic to the number N that is encrypted in an order of appearance of different integers among the inverses to the subsequent integers.

In contrast, the dynamics of elliptic map does not carry any information of this structure at all: For any N, the value q runs only over the set 0, -1, 0, 1.

In hyperbolic case on time intervals less than the return period the sequence q looks like chaotic. Respectively, the inverse Q also walks chaotically over the set of its values masking the mentioned arithmetical structure of N.

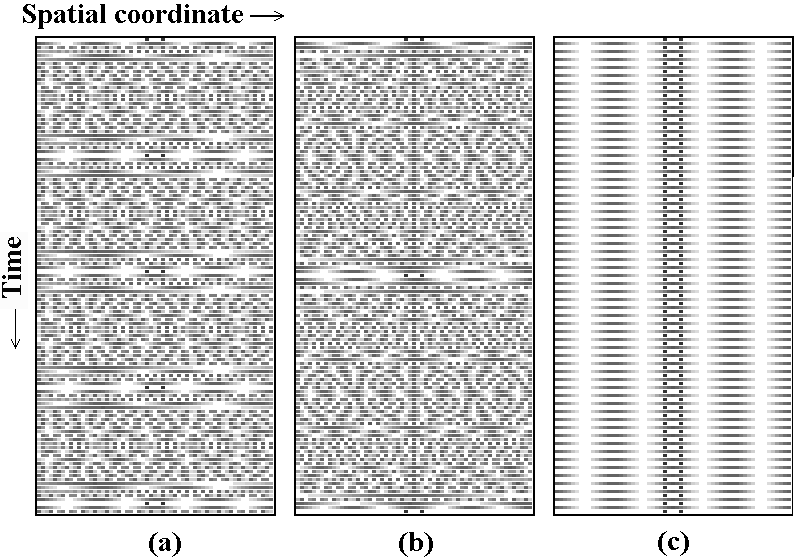
So, the link between quantum and classic dynamics reveals itself in a character of time evolution of spatial period of the interference picture.