
 |
Отображение "кот Арнольда" |
Двумерное отображение

известно в литературе как отображение "кот Арнольда". (Штрих отмечает значения динамических переменных, относящиеся к следующему шагу дискретного времени.) Фазовое пространство этой системы обычно интерпретируют как поверхность тора, на которой одна переменная задают координату по параллели, а другая по меридиану тора, причем обе определены на интервале от 0 до 1. Для графических иллюстраций удобнее использовать единичный квадрат, считая, что расположенные напротив друг друга его стороны отождествляются. Происхождение названия связано с тем, что В.И.Арнольд, предложивший это отображение в качестве примера системы с хаотической динамикой на торе, иллюстрировал его действие, используя картинку в виде головы кота (см. рис.).
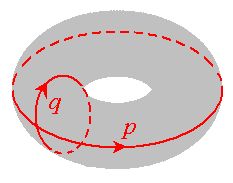

Отображение кота Арнольда относится к классу консервативных систем: при действии отображения любая область (например, голова кота) сохраняет площадь. Известно, что это отображение демонстрирует хаотическую динамику в смысле аксиоматики гиперболической теории Аносова. Два показателя Ляпунова для отображения кота Арнольда
![]()
Отметим, что старший показатель положительный. Некоторые дополнительные сведения об отображении кота Арнольда и других отображениях на торе можно найти в разделе нашего сайта, посвященном квантовому хаосу.
Для дальнейшего полезно заметить, что отображение кота Арнольда можно представить как результат двукратного применения более простого отображения,

В самом деле,

Переходя к вопросу о физической реализации отображения кота Арнольда, рассмотрим четыре связанных неавтономных осциллятора Ван-дер-Поля

Здесь x, y, z и w обобщенные координаты осцилляторов, A - амплитуда модуляции управляющего параметра, T – период модуляции, который, как будем предполагать, содержит целое число периодов собственных колебаний 2p/w0, e - параметр связи.
Система действует следующим образом. Пусть первый и второй осциллятор на стадии генерации совершают колебания с фазами, соответственно, Фx и Фy:
![]()
тогда как вторая пара осцилляторов находится ниже порога генерации. При переходе к стадии возбуждения второй пары, третий осциллятор системы z подвергается воздействию затравочного сигнала, отвечающего произведению xy и содержащего резонансную для этого осциллятора составляющую на удвоенной частоте:
![]()
Таким образом, колебания третьего осциллятора получают фазу Фz=Фx+Фy. Четвертый осциллятор w возбуждается просто сигналом x на частоте w0, так что Фw=Фx. Далее, когда стадия генерации второй пары осцилляторов заканчивается, сигнал w служит затравкой для осциллятора y, вступающего в стадию возбуждения, а сигнал z благодаря смешению с опорным сигналом частоты w0, обеспечивает затравку для осциллятора x, даваемую вторым членом в формуле
![]()
В результате на новой стадии возбуждения первый и второй осцилляторы получают фазы, соответственно, Ф'x=Фz=Фx+Фy и Ф'y=Фw=Фx. Учитывая, что фазы определены с точностью до добавки 2p и вводя нормированные переменные q=Фx/2p и p=Фy/2p, приходим к отображению p'=q, q'=p+q (mod 1), двукратное применение которого, как говорилось выше, эквивалентно отображению кота Арнольда. На следующем рисунке показана зависимость от времени переменных x, y, z и w в системе, совершающей хаотическое движение в соответствии с описанным механизмом. График построен по результатам численного решения уравнений при w0=2p, T=20, A=2, e=0.4.

Хаос проявляет себя в случайном блуждании максимумов и минимумов заполнения относительно огибающей. Чтобы продемонстрировать соответствие динамики фаз отображению кота Арнольда, реализуем следующую процедуру. Будем проводить численное решение уравнений, и в некоторый момент, отвечающий середине стадии возбуждения первого и второго осциллятора, определим их фазы с помощью соотношений

Если точка с координатами (Фx, Фy) попадает в область "головы кота", то изображаем ее на диаграмме, и на двух следующих графиках точки (Фx Фy) через время 2T и 4T. После накопления достаточно большого числа точек, вырисовываются "голова кота" и ее образы после одной и двух итераций отображения Арнольда. Полученные картинки можно сравнить с теми, которые получаются непосредственно из итераций отображения Арнольда. Соответствие достигается в том случае, если ввести в оба уравнения аддитивные константы, которые отвечают определенным постоянным добавкам к фазе, возникающим при эстафетной передаче возмущений между осцилляторами. С учетом этих, подобранных эмпирически для данного режима констант, отображение модифицируется таким образом:

Сравните две приведенные ниже серии диаграмм, чтобы убедиться в замечательном соответствии динамики фаз в предложенной системе и динамики, представленной модифицированным отображением кота Арнольда.


На последнем рисунке приводится график зависимости двух старших показателей Ляпунова для системы связанных неавтономных осцилляторов Ван-дер-Поля от амплитуды медленной модуляции A при фиксированных остальных параметрах, причем за единицу времени принят период 2T.

Как можно видеть, в широком интервале параметра оба показателя Ляпунова остается приблизительно постоянными в хорошем соответствии с величинами, ожидаемыми для отображения кота Арнольда.
Замечание.
Если подходить к описанию динамики рассматриваемой системы формально, с точки зрения построения стробоскопического
отображения Пуанкаре,
то оно сводится к итерациям некоторого 8-мерного отображения.
Действительно, мгновенное состояние системы определяется набором восьми переменных
ЛИТЕРАТУРА
[1] O.B.Isaeva, A.Yu. Jalnine and S.P.Kuznetsov. Arnold's cat map dynamics in a system of coupled nonautonomous van der Pol oscillators. Phys. Rev. E, 74, 2006, 046207
![]()
[2] Д.С. Аржанухина, С.П. Кузнецов. Система трех неавтономных осцилляторов с гиперболическим хаосом. Модель с динамикой на аттракторе, описываемой отображением на торе "кот Арнольда". Известия вузов. Прикладная нелинейная динамика, 20, 2012, №6, 56-66.
![]()