 |
Отображение Бернулли |
 Рассмотрим одномерное отображение
Рассмотрим одномерное отображение
xn+1={2xn}
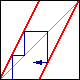
где фигурные скобки обозначают дробную часть числа. Его график и диаграмма, иллюстрирующая динамику на протяжении нескольких итераций, приведены на рисунке.
Удобно представить переменную x в двоичной системе счисления, при этом цифра 0 на первой позиции после разделительной точки отвечает расположению изображающей точки в левой, а 1 - в правой половине единичного интервала. Пусть, например,
x0=0.01011010001010011001010...
Один шаг эволюции во времени состоит в том, что последовательность нулей и единиц сдвигается влево на одну позицию, и цифра, оказавшаяся по левую сторону от разделительной точки, отбрасывается:
x1=0.1011010001010011001010...
x2=0.011010001010011001010...
и так далее. Такое преобразование двоичной последовательности, состоящее в сдвиге всех символов на одну позицию, называют сдвигом Бернулли.
Зададим в качестве начального состояния случайную последовательность цифр, скажем, полученную подбрасыванием монеты, по правилу орел – 0, решка – 1: x0=0.0101101... Тогда при итерациях изображающая точка будет посещать левую или правую половину единичного интервала в точности следуя нашей случайной последовательности. Вот он, хаос!
Ясно, что малое возмущение начального условия за один шаг итераций увеличивается в два раза. Поэтому показатель Ляпунова для данного отображения равен ln 2=0.693.
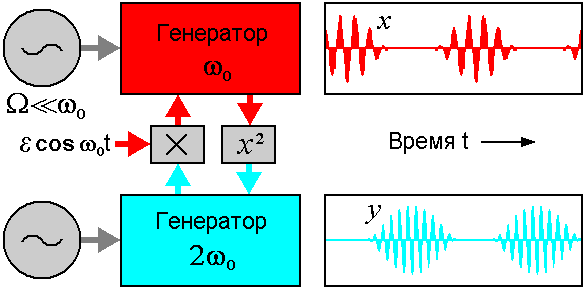
Как реализовать динамику, отвечающую отображению Бернулли, в физической системе? Обратимся к показанной на рисунке блок-схеме. Это неавтономная колебательная система, построенная на базе двух автогенераторов с характерными частотами w0 и 2w0. Параметр, управляющий возбуждением одного и другого генератора, медленно изменяется во времени в противофазе с периодом T, который составляет целое число периодов основной частоты: T=2pN/w0. Таким образом, по очереди возбуждается то один, то другой генератор. Воздействие первого генератора на второй производится через нелинейный квадратичный элемент. Порождаемая вторая гармоника служит затравкой при возбуждении второго генератора. В свою очередь, второй генератор действует на первый через нелинейный элемент, осуществляющий смешение поступающего сигнала и вспомогательного опорного сигнала на частоте w0. При этом появляется составляющая на разностной частоте. Она попадает в резонанс первому генератору и служит затравкой, когда он начинает генерировать. Оба генератора как бы по очереди передают возбуждение один другому.
Поясним, почему схема функционирует как генератор хаоса. Предположим, что на стадии генерации первого осциллятора колебания имеют некоторую фазу j. Сигнал на выходе элемента связи содержит вторую гармонику, и ее фаза 2j передается второму осциллятору, когда он начнет генерировать. Благодаря смешению с опорным сигналом на втором элементе связи, удвоенная фаза передается в исходный частотный диапазон, так что при возбуждении первого осциллятора на очередной стадии генерации он получит фазу 2j. На последовательных стадиях возбуждения первого генератора для его фазы, нормированной на 2p, q=j/2p, будет справедливо отображение Бернулли: qn+1={2qn}.
Чтобы пронаблюдать описанный механизм численно, рассмотрим систему двух осцилляторов Ван-дер-Поля с переменными коэффициентами
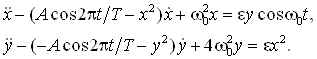
На следующем рисунке показана зависимость от времени переменных x и y в этой системе, совершающей хаотическое движение при эстафетной передаче возбуждения от одного осциллятора к другому. График построен по результатам численного решения уравнений при w0=2p, T=10, A=3, e=0.5.
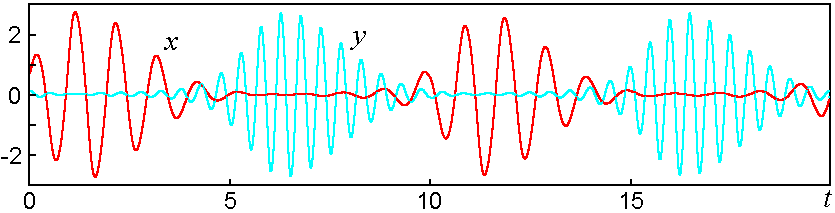
Хаос проявляет себя в случайном блуждании максимумов и минимумов заполнения относительно огибающей. Ниже приводится диаграмма эмпирического отображения для фазы первого осциллятора в середине стадий возбуждения. На графике отложены точки (qn, qn+1) для достаточно большого количества периодов T.

Итак, мы получили отображение, которое несмотря на наличие некоторых деформаций, топологически эквивалентно отображению Бернулли qn+1={2qn}. В самом деле, если мы варьируем исходную фазу так, чтобы изображающая точка один раз обошла полную окружность, то точка-образ совершит двукратный обход окружности. Это выражается в том, что график имеет две ветви, расположенные так же, как на первом рисунке в начале этой страницы. Соответствие с классическим отображением Бернулли становится лучше при увеличении отношения периодов N.
Замечание. Если обратиться к более точным формулировкам, то отображение, определяющее эволюцию состояния системы двух осцилляторов Ван-дер-Поля за период T, четырехмерное. Геометрически его действие состоит в растяжении по фазовой переменной и сильному сжатию по трем остальным направлениям, так что в хорошем приближении отображение оказывается одномерным.
На последнем рисунке представлен график зависимости старшего показателя Ляпунова для системы связанных неавтономных осцилляторов Ван-дер-Поля от амплитуды медленной модуляции A при фиксированных остальных параметрах, причем за единицу времени принят период T.
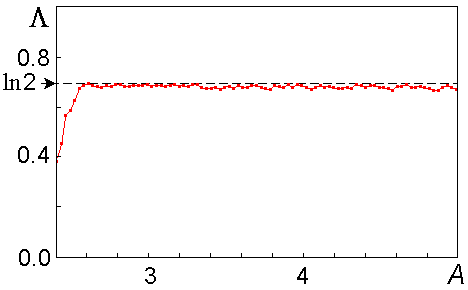
Как можно видеть, в широком интервале параметра показатель Ляпунова остается практически постоянным и приблизительно равен величине ln 2=0.693, отвечающей отображению Бернулли. При малых A соответствие пропадает - показатель Ляпунова становится заметно меньше.
ЛИТЕРАТУРА
[1] S.P.Kuznetsov. Example of a Physical System with a Hyperbolic Attractor of the Smale-Williams Type. Phys. Rev. Lett., 95, 2005, 144101.
![]()
[2] С.П. Кузнецов. Динамический хаос и однородно гиперболические аттракторы: от математики к физике. УФН, 181, 2011, №2, 121-149.
![]()