Для реализации гиперболического хаоса на основе манипуляции фазами колебаний при передаче возбуждения между попеременно возбуждающимися осцилляторами весьма подходящим представляется известный в теории колебаний и приложениях класс параметрических систем. Они могут быть построены на различной физической основе – в электронике, механике, акустике, нелинейной оптике.

Одна из распространенных схем параметрического генератора содержит два парциальных осциллятора, связанных посредством реактивного (бездиссипативного) элемента с изменяющимся во времени параметром. Если собственные частоты осцилляторов w₁, w₂ и частота изменения параметра (частота накачки) w₃ удовлетворяют условию параметрического резонанса w₃=w₁+w₂, то в парциальных осцилляторах возникает одновременная раскачка колебаний. Стабилизация амплитуды может быть достигнута, если ввести, например, нелинейную диссипацию.

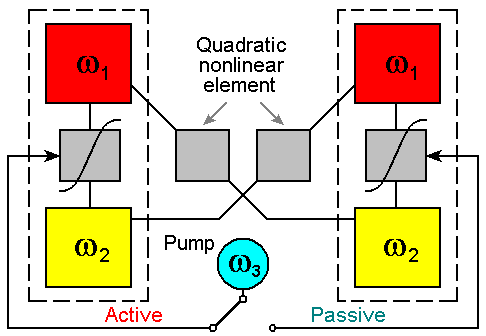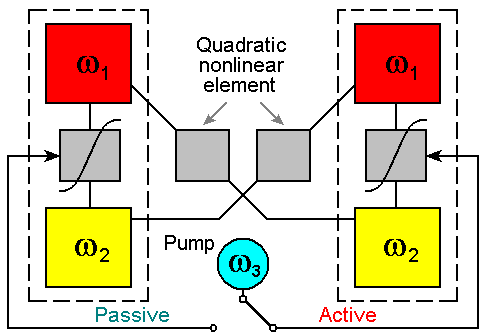Обратимся к системе, составленной из двух таких подсистем A и B [1]. Частоты выберем так, что w₂=2w₁ и w₃=3w₁. (Условие параметрического резонанса, очевидно, выполняется.) Принадлежащий каждой подсистеме осциллятор частоты w₁ полагаем связанным через квадратичный нелинейный элемент с осциллятором частоты w₂, относящимся к подсистеме-партнеру. В силу принятого соотношения частот, воздействие на второй гармонике одного осциллятора на другой будет эффективным – резонансным.

Будем полагать, что накачка включается по очереди в одной и другой подсистеме, так что функционирование устройства состоит в попеременном параметрическом возбуждении подсистем и затухании колебаний в промежутках времени между активными стадиями.

Модель описывается уравнениями

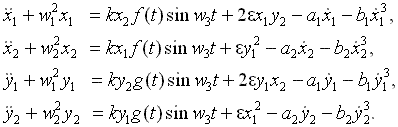
Здесь x_1,2 и y_1,2 – обобщенные координаты двух пар осцилляторов, имеющих собственные частоты w₁ и w₂=2 w₁. Параметр k определяет интенсивность накачки на частоте w₃=3w₁. Параметр e отвечает за нелинейную связь между осцилляторами, относящимися к разным парам. Функции f и g задают медленную зависимость амплитуды накачки от времени, так что для двух пар осцилляторов она совершает колебания в противофазе:

Период модуляции полагаем кратным периоду основной частоты накачки, т.е. T=2pN/w₃, где N - целое.

При N>>1 для описания динамики можно воспользоваться методом медленных амплитуд. Положим

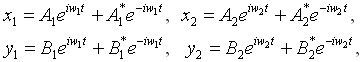
где A и B – медленные комплексные функции времени. После подстановки в уравнения, умножения на экспоненту и усреднения по периоду быстрых колебаний, с учетом принятого соотношения частот w_1,2,3, получаем:

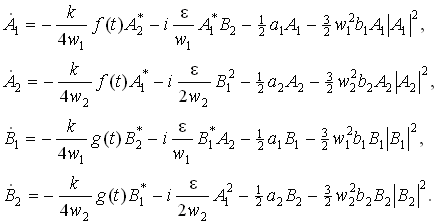
Если e=0, то система распадается на две изолированные подсистемы, A и B.

Рассмотрим одну из них, например, А. (Для второй рассуждения аналогичны.) Без диссипации и при постоянной амплитуде накачки подсистема описывается в терминах комплексных амплитуд уравнениями

На больших временах решение имеет вид

где R и Ф постоянные, определяемые начальными условиями. Это соответствует

Таким образом, возникшие в результате развития параметрической неустойчивости колебания на первой и второй гармонике имеют фазовый сдвиг, задаваемый одной и той же константой Ф, которая зависит от начальных условий. При учете нелинейной диссипации амплитуда колебаний будет претерпевать насыщение, но указанное фазовое соотношение сохранится.

Перейдем к ситуации, когда имеет место попеременное действие накачки на обе подсистемы при наличии ненулевой связи между ними. Возбуждение подсистемы A или B при включении накачки будет происходить в присутствии воздействия со стороны подсистемы-партнера на парциальный осциллятор, имеющий собственную частоту w₂=2w₁. Оно осуществляется посредством порождаемой на нелинейном элементе второй гармоники сигнала от осциллятора, совершающего колебания на частоте w₁. Эта вторая гармоника имеет удвоенную фазу, так что ее же унаследуют колебания возбуждаемого осциллятора, стимулированные этим воздействием. За полный период модуляции накачки трансформация фазы будет приближенно определяться отображением Ф_new=4Ф_old+const (mod 2p), которое относится к семейству отображений Бернулли. Его динамика хаотическая и характеризуется показателем Ляпунова L=ln 4=1.386.

Для аккуратного описания динамики в дискретном времени мгновенное состояние системы в момент t_n следует задать восьмимерным вектором X_n. Решая уравнения на интервале времени T с начальными условиями X_n, получим набор переменных, отвечающий новому состоянию X_n+1. Введем функцию, отображающую восьмимерное пространство в себя: X_n+1=T(X_n). Это отображение Пуанкаре. (В соответствии с известными результатами теории дифференциальных уравнений, оно взаимно однозначное и взаимно дифференцируемое.) Для определения фазовой переменной Ф используем осциллятор на частоте w₁, относящейся к подсистеме, активной в моменты t_n. За одну итерацию отображения Пуанкаре по направлению в восьмимерном пространстве, связанному с фазой Ф, реализуется 4-кратноое растяжение, а по остальным направлениям – сжатие. Отображение Пуанкаре, как мы полагаем, имеет однородно гиперболический хаотический аттрактор, относящийся к семейству соленоидов Смейла – Вильямса.

Обратимся к результатам численного моделирования динамики системы. Удобно принять w₁=2p, w₂=4p, w₃=6p, что соответствует выбору периода собственных колебаний первого осциллятора в одной и другой подсистемах за единицу времени. Ниже на рисунке приводятся типичные образцы временных зависимостей в установившемся режиме параметрической генерации для динамических переменных x и y на протяжении одного периода модуляции накачки при T=40, e=0.5, k=35, a=0.6, b=0.01.

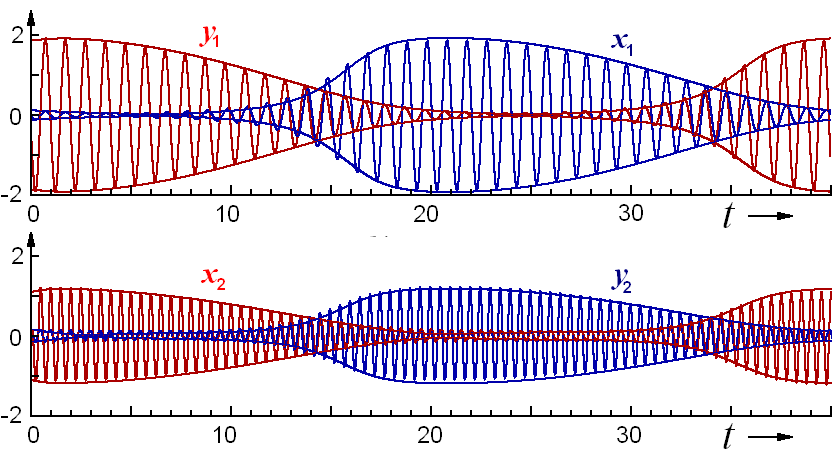
Красным показаны кривые, относящиеся к подсистеме A, а синим – к подсистеме B. Как можно видеть, эволюция во времени состоит в том, что обе подсистемы становятся активными попеременно, соответственно действию накачки. Каждая подсистема выдает сигнал, представляющий собой последовательность импульсов, имеющих высокочастотное заполнение и следующих с периодом модуляции накачки. Однако сигнал в целом непериодический: фаза высокочастотного заполнения меняется от импульса к импульсу хаотически. Приведены также зависимости от времени амплитуд осцилляторов, полученные численным решением амплитудных уравнений. Поскольку оба способа описания хорошо согласуются, далее ограничимся обсуждением динамики в рамках описания амплитудными уравнениями.

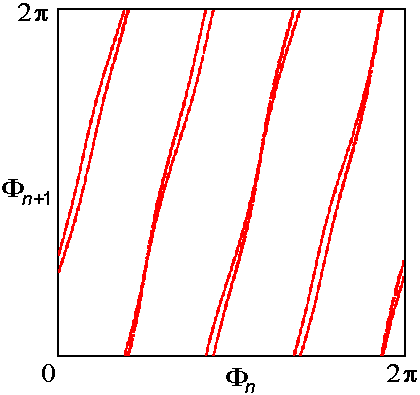На рисунке справа представлена диаграмма для фаз, отвечающих последовательным стадиям возбуждения одной из подсистем. По горизонтальной оси отложена фаза колебаний в подсистеме B, относящаяся к моменту времени t_n=nT, а по вертикали – к моменту времени t_n+1. График построен на основании численного решения амплитудных уравнений. Фаза определяется как Ф_n=argB(t_n). (Подчеркнем, что определение фазы относится к активной стадии рассматриваемой подсистемы, когда амплитуда заведомо далека от нуля.) Как видно из рисунка, однократный обход окружности для прообраза Ф_n четырехкратному обходу для образа Ф_n+1. Это значит, что отображение для фазы относится к тому же топологическому классу, что и отображение Бернулли Ф_new=4Ф_old+const. (Слабое расщепление ветвей графика, по-видимому, несущественно, и им в определенном приближении можно пренебречь.)

Полный спектр показателей Ляпунова для аттрактора, реализующегося в отображении Пуанкаре при указанных выше значениях параметров, согласно результатам расчетов, следующий:

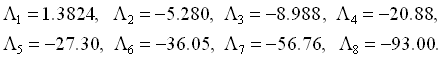
Заметим, что старший показатель хорошо согласуется с величиной ln 4, получаемой при приближенном описании отображением Бернулли. Остальные показатели отрицательные, что говорит о сильном сжатии по прочим направлениям в фазовом пространстве. Оценка фрактальной размерности аттрактора по формуле Каплана – Йорке дает для аттрактора в отображении Пуанкаре D=1.26. Соответственно, для аттрактора исходной системы, вложенного в девятимерное расширенное фазовое пространство, размерность составляет 2.26.

Ниже на рисунке приведен фазовый портрет аттрактора в сечении Пуанкаре в проекции на плоскость динамических переменных первого осциллятора второй подсистемы. На вставке, представляющей фрагмент исходной картинки в увеличенном виде, можно видеть некоторые детали тонкой поперечной фрактальной структуры аттрактора.

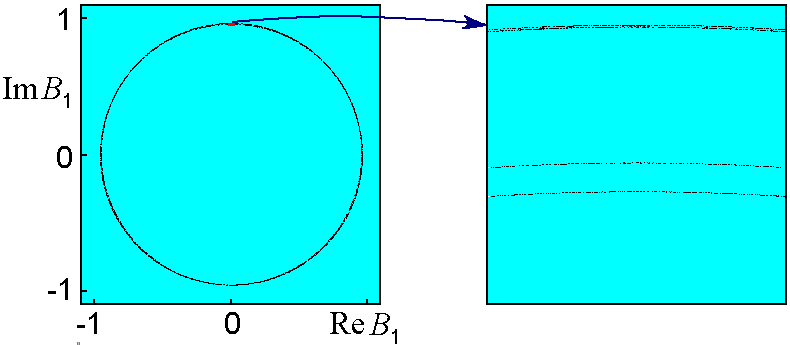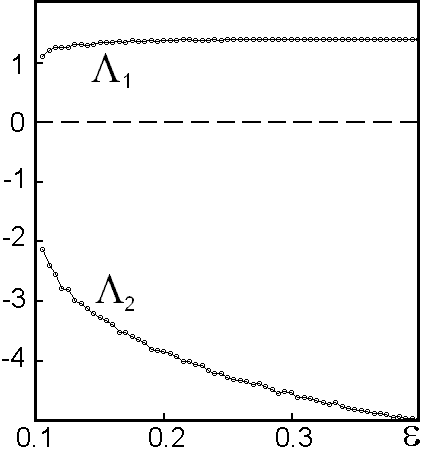На рисунке справа показан график двух наибольших показателей Ляпунова в зависимости от величины связи между подсистемами при фиксированных остальных параметрах. Во всей рассматриваемой области один показатель положительный, а остальные отрицательные. Зависимость от параметра для положительного показателя, отвечающего за присутствие хаоса, гладкая, без каких-либо резких изменений («провалов»). Из рисунка видно, что в широкой области изменения параметра связи величина большего показателя остается близкой к ln 4.

Рассмотренная схема параметрического генератора хаоса открывает возможность получения хаотических режимов нечувствительных к выбору параметров и деталей конструкции в системах различной природы. Одним из возможных приложений может быть использование таких генераторов в схемах скрытой коммуникации на основе хаоса. Другие варианты параметрческих генераторов гиперболического хаоса рассмотрены в работах [2,3].

ЛИТЕРАТУРА

[1] C.П. Кузнецов. О возможности реализации параметрического генератора гиперболического хаоса. ЖЭТФ 133, 2008, №2, 438-446.

[2] А.С. Кузнецов, С.П. Кузнецов, И.Р. Сатаев. Параметрический генератор гиперболического хаоса на основе двух связанных осцилляторов с нелинейной диссипацией. ЖТФ, 80, 2010, вып.12, 1-9.

[3] С.П. Кузнецов. Параметрический генератор грубого хаоса: схемотехническая реализация и моделирование в программной среде Multisim. Вестник СГТУ, 2014, № 3 (76), 34-46.