Математическая теория хаоса, базирующаяся на строгом аксиоматическом фундаменте, имеет дело со странными аттракторами гиперболического типа. У такого аттрактора все принадлежащие ему орбиты в фазовом пространстве системы седловые, причем устойчивое и неустойчивое многообразия (инвариантные множества, составленные из траекторий, приближающихся к исходной в прямом или обратном времени) пересекаются трансверсально, т.е. без касания.

К сожалению, известные физические системы, такие как простые генераторы хаоса, нелинейные осцилляторы с периодическим воздействием и другие, не относятся к классу систем с гиперболическими аттракторами. Хаос в них обычно связан с так называемым квазиаттрактором, который наряду с хаотическими траекториями включает устойчивые орбиты большого периода (не различаемые при решении уравнений на компьютере из-за узости областей притяжения).

Гиперболические странные аттракторы являются грубыми (структурно устойчивыми). Это означает нечувствительность характера движений и взаимного расположения траекторий в фазовом пространстве по отношению к вариации уравнений системы. В отличие от гиперболического аттрактора, для квазиаттракторов характерна чувствительная зависимость деталей динамики от параметров. Это с очевидностью нежелательно для потенциальных приложений хаоса, каковыми являются системы коммуникации, маскировка сигналов и т.д. Таким образом, как с фундаментальной, так и с прикладной точки зрения интересно реализовать гиперболический хаос в физических системах.

В учебниках и монографиях по нелинейной динамике примеры гиперболических аттракторов представлены абстрактными конструкциями. Например, аттрактор Смейла – Вильямса строится для отображения трехмерного пространства в себя, определенного следующей процедурой. Рассмотрим область в форме тора, растянем ее в длину, сложим вдвое и вложим в исходный тор, как показано на рисунке. При каждой следующей итерации количество «витков» удваивается. Объект, который получается в пределе большого числа итераций, называют соленоидом Смейла – Вильямса. Его поперечная структура имеет вид канторова множества.

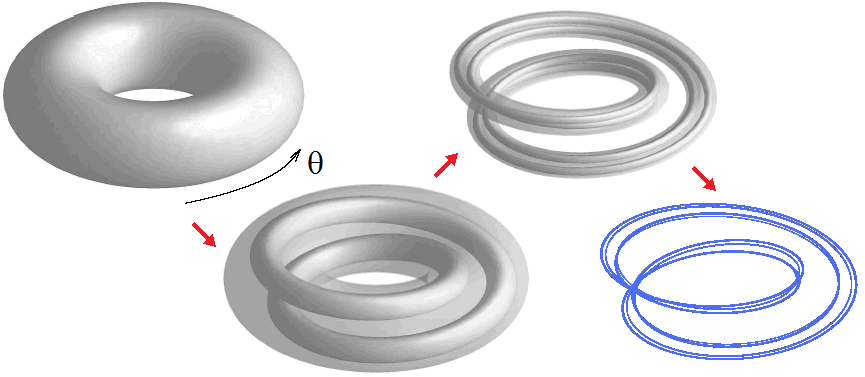
Если ввести угловую координату изображающей точки q, то на последовательных итерациях она, очевидно, подчиняется отображению Бернулли q_n+1={2q_n}. По оставшимся двум направлениям элемент фазового объема претерпевает сжатие. Поэтому подходящим кандидатом с точки зрения реализации аттрактора Смейла - Вильямса представляется система связанных неавтономных генераторов, см. страницу, посвященную отображению Бернулли.

Обратимся к показанной на рисунке схеме радиотехнического устройства [С.П.Кузнецов, Е.П.Селезнев, ЖЭТФ, 2006, №2].

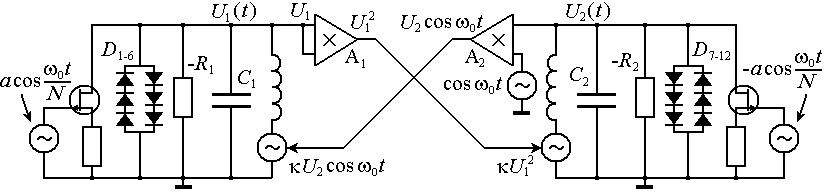
Каждая из двух подсистем - генераторов содержит колебательный контур, образованный катушкой индуктивности L_1,2 и емкостью C_1,2, причем собственная частота второго вдвое больше, чем первого. Отрицательное сопротивление -R_1,2 вносится элементом на основе операционного усилителя. Увеличение потерь энергии с ростом амплитуды колебаний обеспечивается нелинейным элементом, составленным из полупроводниковых диодов. Полевой транзистор вносит положительную проводимость, величина которой регулируется напряжением, подаваемым на затвор. Оно медленно изменяется во времени с периодом T в противофазе для первого и второго генератора, что обеспечивает их поочередное возбуждение. Первый генератор действует на второй через нелинейный квадратичный элемент A₁, порождающий вторую гармонику, а второй на первый через нелинейный элемент A₂, осуществляющий смешение второй гармоники и вспомогательного сигнала на частоте w₀.

Чтобы описать динамику предлагаемой схемы, для каждой подсистемы выпишем уравнение Кирхгофа, выражающее равенство нулю суммарного тока в параллельных ветвях схемы, и уравнение, связывающее напряжение и ток через катушку индуктивности. После замены переменных, обеспечивающей приведение к безразмерной форме, получаем:

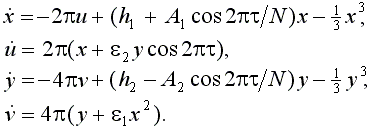
Здесь безразмерные переменные x и u характеризуют напряжение и ток в колебательном контуре первого генератора (соответственно, U₁ и I₁), а y и v - напряжение и ток во втором колебательном контуре (U₂ и I₂). Время нормировано на период собственных колебаний первого контура. Параметры A₁ и A₂ определяют амплитуду медленной модуляции параметра, отвечающего за бифуркацию Андронова - Хопфа в первом и втором генераторе, а h₁ и h₂ смещение среднего значения этого параметра относительно точки бифуркации. Наконец, e₁ и e₂ - это параметры связи между подсистемами.

Мы можем рассматривать динамику стробоскопически, отслеживая дискретную последовательность мгновенных состояний системы с периодом T. Это сводится к итерациям некоторого 4-мерного отображения. Действительно, мгновенное состояние системы определяется набором четырех переменных V={x,u,y,v}. Если в некоторый момент t=nT задан вектор состояния V_n, то из решения уравнений можно однозначно определить состояние через период T: V_n+1=F(V_n). В четырехмерном пространстве направление, связанное с фазой колебаний q (определенной, скажем, на стадии возбуждения для первого осциллятора) отвечает расширению, а три остальных направления – сжатию. Геометрически мы можем вообразить тороид в четырехмерном пространстве и связать одну итерацию отображения с продольным растяжением и поперечным сжатием этого объекта, который затем вкладывается дважды сложенным внутрь исходной области. Это точно соответствует конструкции гиперболического аттрактора Смейла – Вильямса, правда, в четырехмерном, а не трехмерном пространстве.

Описанная система была реализована в виде лабораторного устройства, причем собственные частоты колебательных контуров были равны приблизительно 1 и 2 кГц. Напряжения U₁ и U₂, снимаемые, соответственно, с первого и второго контура, можно было подавать на регистрирующую аппаратуру (осциллограф, анализатор спектра) или вводить в компьютер в виде временного ряда через посредство аналого-цифрового преобразователя. Производную по времени получали как результат аналогового дифференцирования с использованием стандартной дифференцирующей цепочки, содержащей емкость, резистор и операционный усилитель.

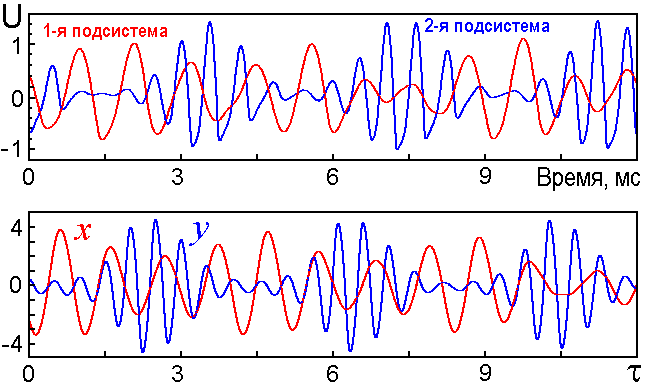
В эксперименте при надлежащем подборе параметров в системе наблюдались хаотические колебания, обусловленные эстафетной передачей возбуждения от одного осциллятора к другому. На рисунке показаны типичные образцы временных зависимостей напряжения в режиме хаотической генерации в одной и другой подсистеме при отношении частоты медленного изменения параметров и частоты вспомогательного сигнала N=4, - в эксперименте и по результатам численного решения системы уравнений. Экспериментальный график построен на компьютере с использованием записанных в память временных рядов, полученных посредством аналого-цифрового преобразования напряжений U₁(t) и U₂(t).

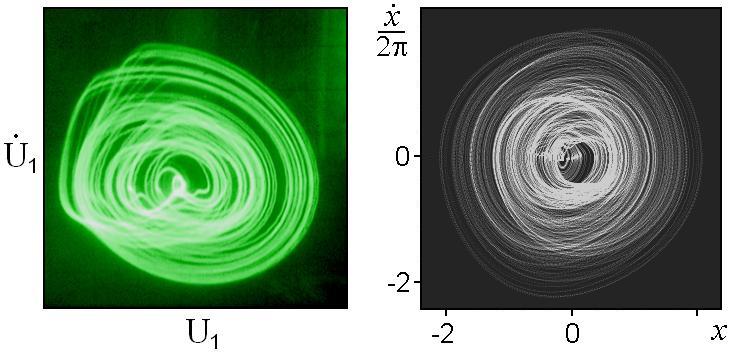
Следующая пара рисунков показывает портреты аттрактора в проекции на плоскость, где по осям координат отложены обобщенная координата (напряжение) и скорость (производная по времени от напряжения) для первого осциллятора. Цветной портрет аттрактора сфотографирован непосредственно с экрана осциллографа. Второй портрет получен из решения уравнений на компьютере. Он представлен в серых тонах, где яркость изображения пропорциональна относительному времени пребывания в соответствующих точках.

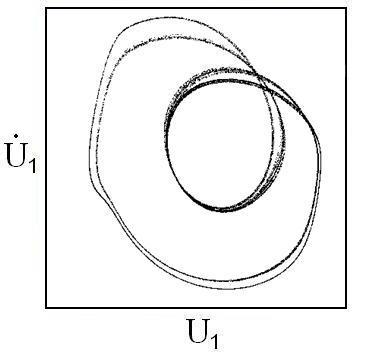
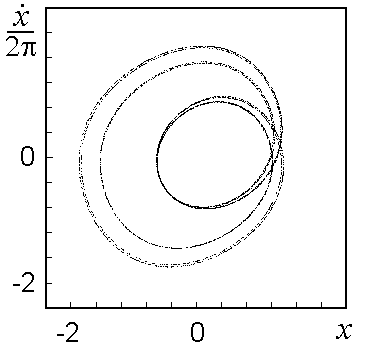
Чтобы увидеть структуру, присущую аттрактору Смейла - Вильямса, нужно обратиться к портрету аттрактора в стробоскопическом сечении, где отображены точки через период внешнего воздействия T. Первая диаграмма получена в эксперименте, а вторая - по результатам численного решения системы уравнений. Портрет выглядит именно так, как должен выглядеть соленоид Смейла - Вильямса, причем хорошо видна фрактальная поперечная структура.

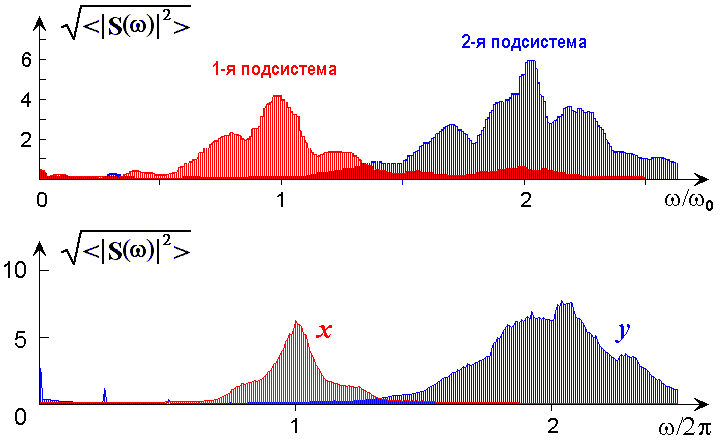
На последнем рисунке представлены спектры Фурье первого и второго осциллятора. Первый рисунок получен в эксперименте фотографированием с экрана анализатора спектра, а второй построен по результатам решения уравнений на компьютере. Отметим очевидную из рисунка непрерывную зависимость спектральной плотности мощности от частоты и отсутствие сильной «изрезанности», характерной обычно для спектров, порождаемых негиперболическими аттракторами.

В целом представленные результаты позволяют уверенно утверждать, что и в эксперименте, и в теоретическом рассмотрении мы имеем дело с одним и тем же объектом - странным аттрактором типа Смейла – Вильямса в неавтономной колебательной системе.

Недавно получено математическое обоснование гиперболической природы хаотического аттрактора в системе дифференциальных уравнений, отвечающих рассмотренной схеме двух попеременно активных осцилляторов, передающих возбуждение друг другу. [Daniel Wilczak. Uniformly Hyperbolic Attractor of the Smale–Williams Type for a Poincare Map in the Kuznetsov System . SIAM J. Applied Dynamical Systems, 9, 2010, No. 4, 1263–1283] ( Preprint arXiv:1006.0614)

Появление примера физической системы с гиперболическим хаотическим аттрактором имеет принципиальное значение для дальнейшего развития нелинейной динамики и ее приложений. Это в определенном смысле, «прорыв в гиперболическую область». Опираясь на присущее гиперболическим аттракторам свойство грубости, можно строить и другие примеры систем с гиперболическим хаосом. Наличие таких физических систем открывает возможности для приложений глубоко проработанного раздела математики – гиперболической теории, а также переводит в практическую плоскость задачу сравнительного исследования гиперболического и негиперболического хаоса в теории и эксперименте.

ЛИТЕРАТУРА

[1] C.П. Кузнецов, Е.П. Селезнёв. Хаотическая динамика в физической системе со странным аттрактором типа Смейла – Вильямса. ЖЭТФ, 129, 2006, №2, 400-412.

[2] С.П. Кузнецов. Динамический хаос и однородно гиперболические аттракторы: от математики к физике. УФН, 181, 2011, №2, 121-149.