Как известно, в линейном приближении колебания струны описываются уравнением в частных производных

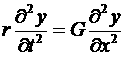
где y(x,t) – поперечное смещение струны в точке с координатой x в момент t, r – линейная плотность струны (масса на единицу длины), G – сила натяжения. Для однородной струны при постоянном натяжении величина c=(G/r)^1/2 определяет скорость распространения волновых возмущений.

Закрепленная на концах струна длины L имеет набор собственных мод с частотами f_n=nc/L. В классическом опыте Мельде при периодическом изменении во времени силы натяжения струны с частотой 2f₀, где f₀ отвечает одной из мод, возбуждаются параметрические колебания на этой моде; при этом в уравнении струны коэффициент G является функцией времени периода 1/2f₀, и это линейное уравнение описывает начальную стадию развития параметрической неустойчивости. Колебания силы натяжения выступают в качестве накачки – источника энергии, обеспечивающего параметрическое возбуждение.

Если использовать накачку попеременно на частотах, различающихся втрое, то можно обеспечить параметрическое возбуждение коротковолновых и длинноволновых паттернов по очереди, с передачей пространственной фазы от одного паттерна к другому так, чтобы за полный период модуляции накачки имело место утроение фазовой переменной [1, 2]. При наличии диссипации сжатие по остальным направлениям в пространстве состояний системы обеспечивает присутствие аттрактора типа Смейла – Вильямса. Концептуально проще всего осуществить эту идею для системы с периодическими граничными условиями, т.е. замкнутой в кольцо (хотя это и не самой простой вариант для воспроизведения в эксперименте).

Пусть сила натяжения струны колеблется по закону

где коэффициенты a₂, a₆ изменяются во времени с некоторым периодом T, поочередно оказываясь по величине большими или близкими к нулю. Конкретно, мы задаем

Таким образом, накачка имеет составляющие на частотах 2w₀ и 6w₀ с амплитудами, модулированными во времени. Распределение массы по струне будем считать слабо неоднородным, зависящим от пространственной координаты по закону

где k₀=w₀/c₀, c₀=(G₀/r₀)^1/2 Кроме того, введем линейную и нелинейную диссипацию, добавив в правую часть уравнения нелинейный член, пропорциональный производной по времени. Присутствие нелинейной диссипации необходимо для стабилизации параметрической неустойчивости, однако для рассматриваемой здесь системы существенным является еще и то обстоятельство, что кубическая нелинейность обеспечивает возникновение третьей гармоники при колебательно-волновых движениях. Наконец, добавим линейный член, отвечающий за затухание колебательно-волновых возмущений с нулевым волновым числом. Используя нормировку переменных и параметров такую, что c₀=1, k₀=w₀, приходим к системе, описываемой уравнением в частных производных следующего вида:

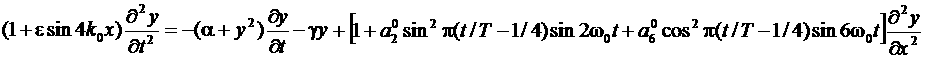
Наложим на систему периодические граничные условия

Механизм функционирования системы состоит в следующем.

Предположим, что при накачке на частоте 2w₀ в системе возбуждается стоячая волна на частоте w₀ с волновым числом k₀, у которой расположение узлов и пучностей характеризуется фазовой постоянной Ф, так что в грубом приближении y~cosw₀t sin(k₀x+Ф). Амплитуда стабилизируется на конечном уровне благодаря нелинейной диссипации. Также из-за ее присутствия колебательно-волновое движение будет иметь составляющую на третьей гармонике вида sin 3w₀t sin(3k₀x+3Ф).

Затем имеет место стадия, когда амплитуда накачки на частоте 2w₀ становится малой, и колебания частоты w₀ затухают. С другой стороны, амплитуда накачки на частоте 6w₀ теперь достаточна для развития параметрической неустойчивости стоячей волны с частотой 3w₀ и волновым числом 3k₀. Эта волна формируется из возмущения, оставшегося от предыдущей стадии процесса, и поэтому характеризуется пространственной фазой 3Ф.

Далее, вновь наступает стадия накачки на частоте 2w₀, и коротковолновый паттерн затухает. Затравочное колебательно-волновое возбуждение параметрических колебаний с частотой w₀ и волновым числом k₀ обеспечивается теперь благодаря возмущению sin 3w₀t sin(3k₀x+3Ф), оставшемуся от предыдущей стадии процесса в комбинации с составляющей частоты 2w₀ и с волновым числом 4k₀, которая присутствует из-за наличия накачки и пространственной зависимости плотности струны (ее пространственная фаза фиксирована). В результате новая величина сдвига пространственной фазы возникающего паттерна Ф' получается как результат применения троекратно растягивающего отображения окружности вида Ф'=-3Ф+const. Это отображение с хаотической динамикой, характеризуемое положительным показателем Ляпунова L=ln3=1.0986...

По остальным направлениям в фазовом пространстве отображения, описывающего изменение состояния системы за период модуляции накачки, будет происходить сжатие, что обеспечивает реализацию аттрактора типа Смейла – Вильямса.

Для параметров

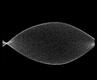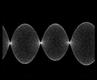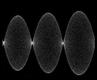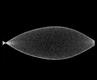
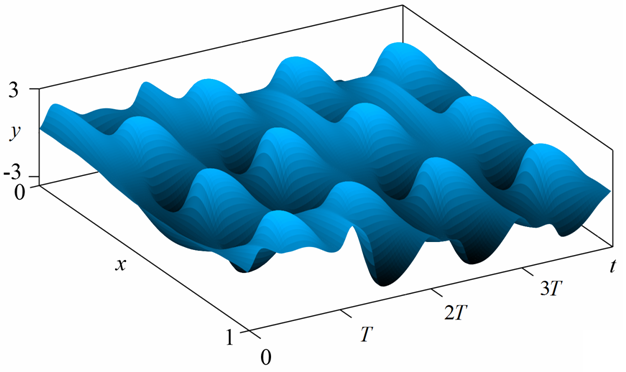
результаты численного решения уравнения с частными производными представлены в виде анимации, показывающей эволюцию стоячих волн на струне во времени, и 3D диаграммы, где пространственное распределение выводится с временным шагом, отвечающим периоду быстрых колебаний (так что высокочастотного заполнения не видно). Можно видеть, что в системе поочередно возбуждаются длинноволновые и коротковолновые структуры, притом пространственная фаза их меняется от одного периода модуляции накачки к другому.

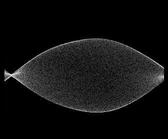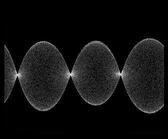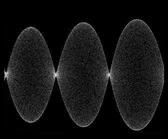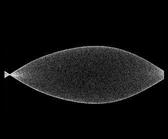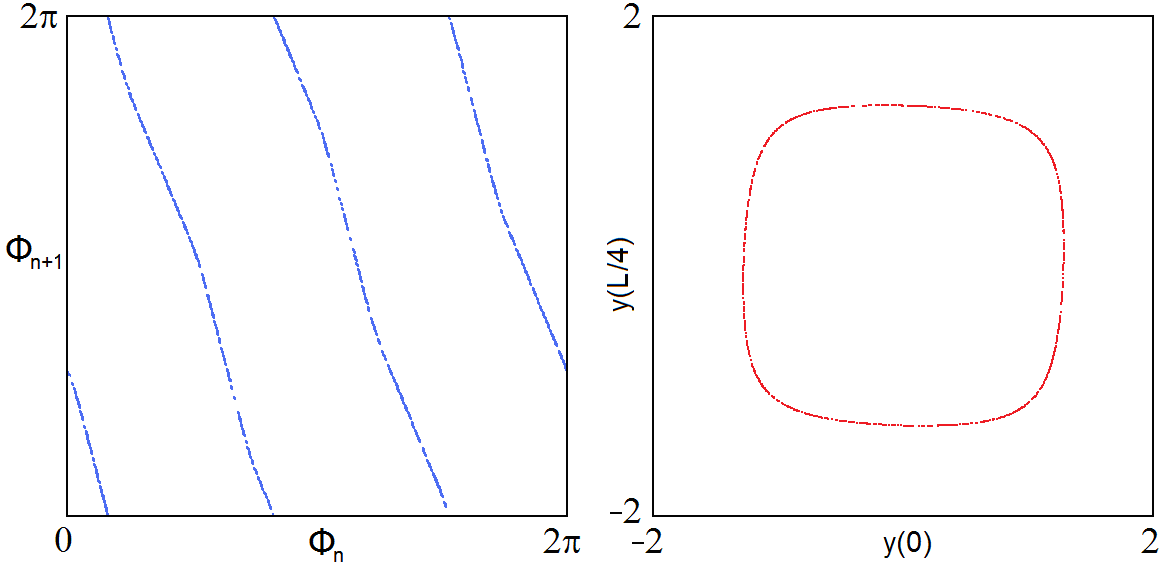
Можно проверить, что за период модуляции накачки пространственная фаза стоячих волн действительно претерпевает трехкратно растягивающее отображение окружности, для чего в процессе решения уравнения на компьютере на большом числе периодов модуляции вычисляем пространственные фазы в моменты времени t_n=nT. Представив результаты графически в координатах Ф_n, Ф_n+1, видим, что расположение ветвей получается таким, что однократный обход окружности для прообраза соответствует трехкратному обходу для образа в обратном направлении. Приведенный рядом рисунок иллюстрирует портрет аттрактора в стробоскопическом сечении в проекции на плоскость переменных смещения струны в точках, отстоящих одна от другой на четверть основной длины волны. Это соленоид Смейла-Вильямса, хотя поперечная фрактальная структура не видна из-за сильного поперечного сжатия, и изображение выглядит как замкнутая кривая, но расположение изображающих точек на последовательных шагах итераций отображения Пуанкаре отвечает скачкам на этой кривой, в соответствии с троекратно растягивающим отображением окружности.

Учитывая, что параметрическое возбуждение стоячих волн имеет место на волновых числах k₀ и 3k₀, можно построить редуцированную конечномерную модель, в которой в качестве динамических переменных будут выступать зависящие от времени коэффициенты разложения решения по соответствующим пространственным модам. Это система обыкновенных дифференциальных уравнений 12 порядка довольно громоздкая, и здесь не приводится. Ее можно найти в работе [3], где показано, что результаты численного решения редуцированной системы уравнений, по крайней мере в определенной представляющей интерес области параметров, хорошо согласуются с расчетами для системы в частных производных. Кроме того, в работе [3] рассмотрены ситуации параметрического возбуждения паттернов стоячих волн также при других отношениях частот, когда фактор растяжения для фазовой переменной определяется нечетными числами от 3 до 11.

В работах [1, 2] показано, что гиперболический аттрактор можно реализовать также в системе с фиксацией концов струны. Это удается обеспечить при увеличении длины системы и введении зависимости линейной диссипации от пространственной координаты по определенному профилю, с увеличением параметра диссипации у концов струны.

Страница разработана при поддержке гранта РНФ 15-12-20035, выполняемого в Удмуртском государственном университете (Ижевск).

ЛИТЕРАТУРА

[1] Isaeva O.B., Kuznetsov A.S., Kuznetsov S.P. Hyperbolic chaos of standing wave patterns generated parametrically by a modulated pump source. Phys. Rev. E. 2013. V. 87, 040901.

[2] Исаева О.Б., Кузнецов А.С., Кузнецов С.П. Гиперболический хаос при параметрических колебаниях струны. Нелинейная динамика. 2013. Т. 9. №1, 3-10.

[3] Круглов В.П., Кузнецов А.С., Кузнецов С.П. Гиперболический хаос в системах с параметрическим возбуждением паттернов стоячих волн. Нелинейная динамика. 2014. Т. 10. №3, 265-277.