
 |
Множества Мандельброта и Жюлиа |
Один из глубоко проработанных математиками разделов нелинейной динамики имеет своим содержанием исследование итерируемых отображений, заданных аналитическими функциями комплексного переменного. Классическим объектом служит комплексное квадратичное отображение
![]()
Если с=0, имеет место очевидное поведение: при |z0|>1 результат последовательных итераций будет стремиться к бесконечности, а при |z0|<1 оставаться в ограниченной области. Границей между этими двумя типами поведения служит единичная окружность |z0|=1. При других значениях комплексного параметра c множество на комплексной плоскости z, разграничивающее эти типы поведения, устроено, вообще говоря, сложным и нетривиальным образом. Его называют множеством Жюлиа (см. примеры на рисунке).
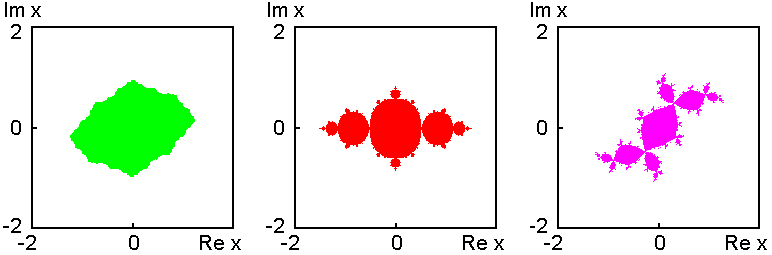
 С другой стороны, если мы фиксируем начальное условие
z0=0 и рассмотрим поведение в зависимости от комплексного параметра c,
то при одних его значениях итерации будут убегать на бесконечность,
а при других оставаться в ограниченной области.
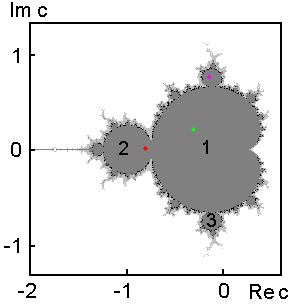
Ассоциирующееся с этой последней ситуацией множество точек на комплексной плоскости
c называется множеством Мандельброта (см. рисунок справа). Цифры 1, 2, 3
обозначают период динамики, наблюдаемой в нескольких основных лепестках "кактуса".
Цветными точками отмечены
значения параметра, для которых получены портреты множеств Жюлиа на предыдущем рисунке.
С другой стороны, если мы фиксируем начальное условие
z0=0 и рассмотрим поведение в зависимости от комплексного параметра c,
то при одних его значениях итерации будут убегать на бесконечность,
а при других оставаться в ограниченной области.
Ассоциирующееся с этой последней ситуацией множество точек на комплексной плоскости
c называется множеством Мандельброта (см. рисунок справа). Цифры 1, 2, 3
обозначают период динамики, наблюдаемой в нескольких основных лепестках "кактуса".
Цветными точками отмечены
значения параметра, для которых получены портреты множеств Жюлиа на предыдущем рисунке.
Замечание. Комплексным отображениям посвящен также специальный раздел нашего сайта.
Идея физической реализации феноменов комплексной динамики, которую мы здесь предлагаем, опирается на известный в теории колебаний и волн
метод комплексных амплитуд. Пусть имеем колебательный процесс на частоте
w0 с медленно меняющейся комплексной амплитудой
a(t):
Рассмотрим систему двух связанных неавтономных осцилляторов
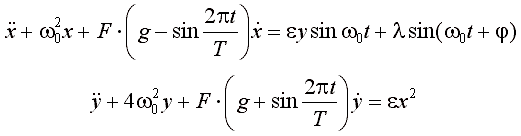
Первый из них имеет собственную частоту w0, а второй вдвое большую. Параметр, управляющий диссипацией в одном и другом осцилляторе, медленно изменяется во времени в противофазе с периодом T, составляющем целое число периодов собственных колебаний.
Параметр g принимается положительным, меньшим единицы. Поэтому, будучи в среднем положительной,
на определенной части периода модуляции диссипация для одного или другого осциллятора
становится отрицательной. На этом участке осциллятор активный (колебания нарастают), а на остальной части периода диссипативный (колебания затухают).
 Предположим, к моменту начала активной стадии второго осциллятора первый совершает колебания с комплексной амплитудой a:
x(t)~Re[a(t)exp(iw0t)].
Воздействие на второй осциллятор производится через нелинейный квадратичный элемент, и «затравкой» для его колебаний будет попадающая в резонанс составляющая на второй гармонике,
Re[a2exp(2iw0t)].
Поэтому комплексная амплитуда колебаний второго осциллятора на активной стадии пропорциональна
a2. Смешение с опорным сигналом (см. правую часть первого уравнения) приводит к появлению составляющей на разностной частоте w0, амплитуда которой пропорциональна a2. В сумме с дополнительным колебательным членом на частоте
w0, характеризуемым амплитудой
l и фазой j, это дает «затравку» для комплексной амплитуды первого осциллятора вида a2 плюс комплексная константа.
Таким образом, стробоскопическое отображение для комплексной амплитуды
будет соответствовать, по крайней мере в определенном приближении,
комплексному квадратичному отображению.
При этом роль комплексного параметра c
играет комплексное число с модулем l и аргументом
j. В зависимости от этого параметра, может случиться, что
решение уравнений связанных неавтономных осцилляторов остается ограниченным
при выборе начальных условий в какой-то области фазового пространства, или может оказаться
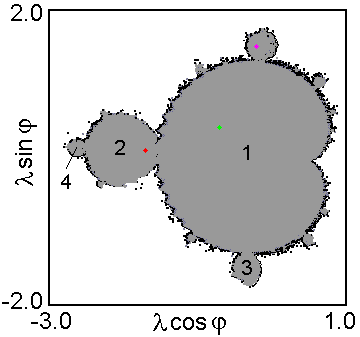
убегающим на бесконечность. На рисунке справа приводится полученная численно диаграмма,
где серым цветом отмечены точки, отвечающие динамике в ограниченной области.
Расчеты проведены для значений параметров
w0=2p,
T=10, F=7, g=0.5, e=1.
Объект на диаграмме демонстрирует очевидное
сходство с множеством Мандельброта для комплексного квадратичного отображения.
Цифры 1, 2, 3 обозначают "лепестки", где реализуется динамика периода, соответственно,
T, 2T, 3T.
Предположим, к моменту начала активной стадии второго осциллятора первый совершает колебания с комплексной амплитудой a:
x(t)~Re[a(t)exp(iw0t)].
Воздействие на второй осциллятор производится через нелинейный квадратичный элемент, и «затравкой» для его колебаний будет попадающая в резонанс составляющая на второй гармонике,
Re[a2exp(2iw0t)].
Поэтому комплексная амплитуда колебаний второго осциллятора на активной стадии пропорциональна
a2. Смешение с опорным сигналом (см. правую часть первого уравнения) приводит к появлению составляющей на разностной частоте w0, амплитуда которой пропорциональна a2. В сумме с дополнительным колебательным членом на частоте
w0, характеризуемым амплитудой
l и фазой j, это дает «затравку» для комплексной амплитуды первого осциллятора вида a2 плюс комплексная константа.
Таким образом, стробоскопическое отображение для комплексной амплитуды
будет соответствовать, по крайней мере в определенном приближении,
комплексному квадратичному отображению.
При этом роль комплексного параметра c
играет комплексное число с модулем l и аргументом
j. В зависимости от этого параметра, может случиться, что
решение уравнений связанных неавтономных осцилляторов остается ограниченным
при выборе начальных условий в какой-то области фазового пространства, или может оказаться
убегающим на бесконечность. На рисунке справа приводится полученная численно диаграмма,
где серым цветом отмечены точки, отвечающие динамике в ограниченной области.
Расчеты проведены для значений параметров
w0=2p,
T=10, F=7, g=0.5, e=1.
Объект на диаграмме демонстрирует очевидное
сходство с множеством Мандельброта для комплексного квадратичного отображения.
Цифры 1, 2, 3 обозначают "лепестки", где реализуется динамика периода, соответственно,
T, 2T, 3T.
Следующий рисунок иллюстрирует характер динамики системы в одном из режимов, соответствующем лепестку периода 3. Показаны зависимости от времени для переменных x и y, отвечающих двум связанным неавтономным осцилляторам.
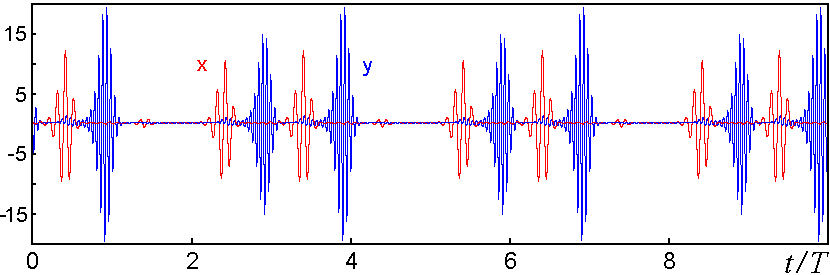
Очевидно, тип режима определяется тем, какой будет на участке минимальной амплитуды колебаний первого осциллятора сигнал "затравки", представляющий собой суперпозицию трансформированного на нелинейном элементе сигнала от осциллятора-партнера и внешнего сигнала. При этом существенны детали соотношения фаз этих двух сигналов, что и определяет тонкую структуру лепестков "кактуса" на плоскости параметров.
Для точек, отмеченных на рисунке "кактуса" цветными метками, построены диаграммы на плоскости переменных первого осциллятора (x, dx/dt), изображающие бассейны аттрактора, расположенного в ограниченной области. Их можно сопоставить с портретами множеств Жюлиа для квадратичного отображения на самом первом рисунке этой страницы.
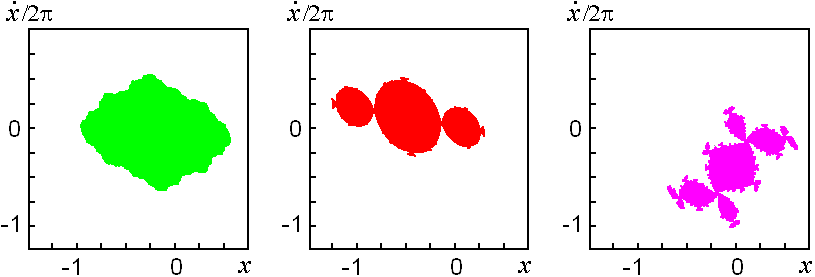
Приведенные данные убедительно демонстрируют характерные для комплексной аналитической динамики феномены: по крайней мере, в общих чертах воспроизводятся такие объекты как множества Мандельброта и Жюлиа. Вопрос о том, распространяется ли соответствие на фрактальную структуру объектов в сколь угодно малых масштабах, требует дальнейших исследований.
ЛИТЕРАТУРА
[1] С.П. Кузнецов, О.Б. Исаева, А. Осбалдестин. Феномены комплексной аналитической динамики в системе связанных неавтономных осцилляторов с поочередным возбуждением. Письма в ЖТФ, 33, 2007, вып.17, 69-76.
![]()
[2] O.B. Isaeva, S.P. Kuznetsov and A.H. Osbaldestin. A system of alternately excited coupled non-autonomous oscillators manifesting phenomena intrinsic to complex analytical maps. Physica D237, 2008, 873–884.
![]()