

|
Аттрактор Плыкина |
В теории динамических систем вводится в рассмотрение класс однородно гиперболических аттракторов. Это аттракторы, составленные исключительно из траекторий седлового типа, причем их устойчивые и неустойчивые многообразия не имеют касаний, а пересекаться могут только трансверсально. Эти аттракторы обладают сильными хаотическими свойствами и допускают подробный математический анализ. Одно из их важнейших свойств – грубость или структурная устойчивость. В учебниках и монографиях по нелинейной динамике примеры гиперболических аттракторов представлены абстрактными конструкциями, такими как аттракторы Плыкина и Смейла – Вильямса. Простейший аттрактор типа Плыкина строится на плоскости при отображении области с дырками в себя, как показано на рисунке.
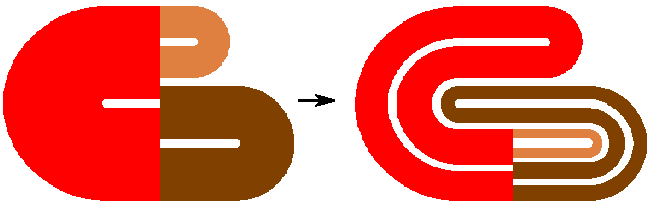
Хотя основные положения теории сформулированы около 40 лет назад, до последнего времени гиперболические аттракторы рассматривались скорее как рафинированный образ динамического хаоса, нежели как относящиеся к динамике реальных систем. Было бы интересно иметь примеры аттракторов такого типа в физике, технике, других дисциплинах.
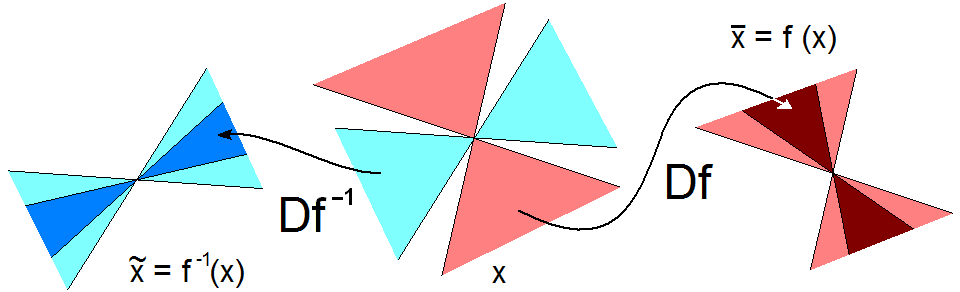
Для построения системы с аттрактором Плыкина [1,2] рассмотрим сначала отображение сферы в себя, заданное последовательностью непрерывных преобразований из четырех периодически повторяющихся стадий. Протяженность одной стадии принята за единицу времени. Роль дырок будут играть окрестности точек A, B, C, D на сфере. Первую стадию определим как сток изображающих точек по параллелям, в направлении от меридианов AB и DC. Вторая стадия – дифференциальное вращение вокруг оси z с угловой скоростью, линейно зависящей от z, так, что точки B и C остаются на месте, а точки A и D меняются местами. Третья и четвертая стадия отличаются от первых двух только пространственной ориентацией – меняются ролями оси x и z. На рисунке преобразования иллюстрируются геометрически, и приведен вид дифференциальных уравнений для каждой стадии.
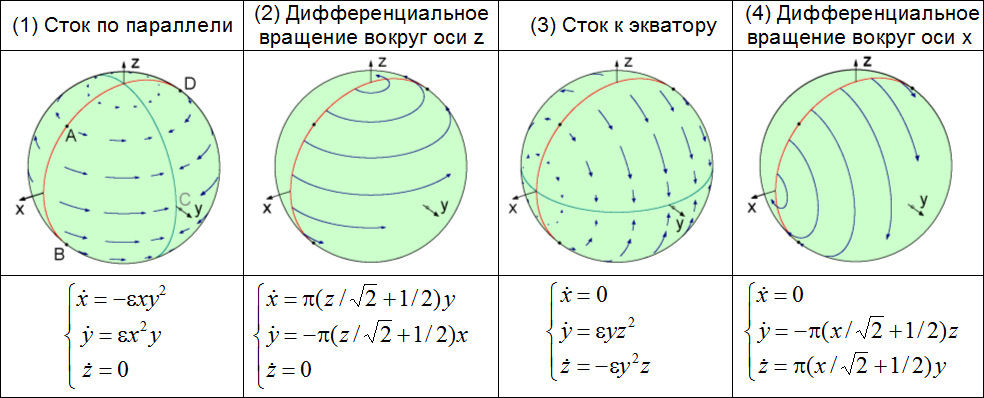
Интуитивно кажется резонным, что такой поток будет формировать вытянутые волокна с тонкой поперечной структурой, характерной для аттрактора Плыкина. Трансформация состояния за полный цикл описывается отображением
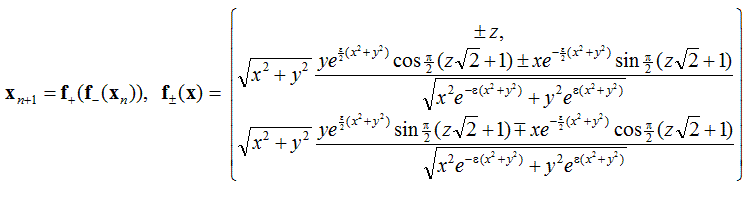
При e=1 итерации этого отображения на компьютере имеют результатом показанный на рисунке аттрактор. Обратим внимание на характерную поперечную фрактальную структуру: объект состоит из полосок, внутри которых имеются полоски следующего уровня и так далее. В непрерывном времени эволюция структуры иллюстрируется роликом.
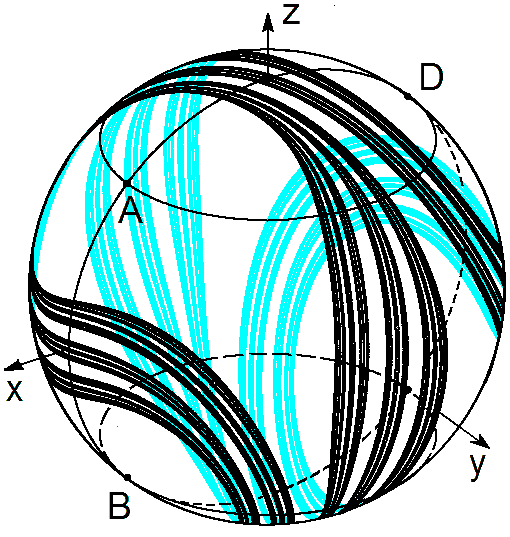
|

|
От представления состояний точками на сфере можно перейти на плоскость, используя стереографическую проекцию, которая дается заменой переменных
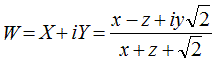
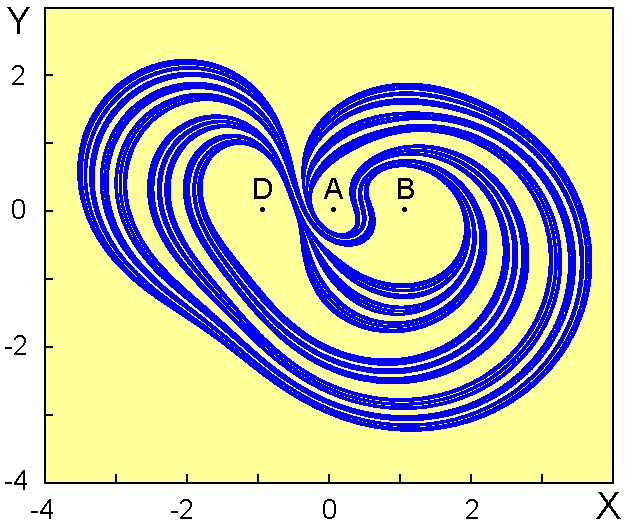
За центр проецирования взята точка C, которая не принадлежит аттрактору, так что на плоскости объект расположен в ограниченной области, как показано на рисунке. Если говорить об аттракторе потоковой системы, то он располагается в расширенном фазовом пространстве (X, Y, t). При перемещении секущей плоскости (X,Y) вдоль временной оси имеет место эволюция объекта в сечении, иллюстрируемая роликом. Из этой картинки усматривается суть гиперболической природы аттрактра: в процессе эволюции вдоль волокон все время происходит растяжение, а поперек структуры волокон - сжатие.
|

|
Учитывая структурную устойчивость гиперболического аттрактора, можно модифицировать систему уравнений в надежде, что это не изменит природу аттрактора. В частности, перейти от коэффициентов кусочно-непрерывных во времени к гладким коэффициентам. Обратимся к следующей системе уравнений, которая выписана в переменных, задающих координаты на плоскости:
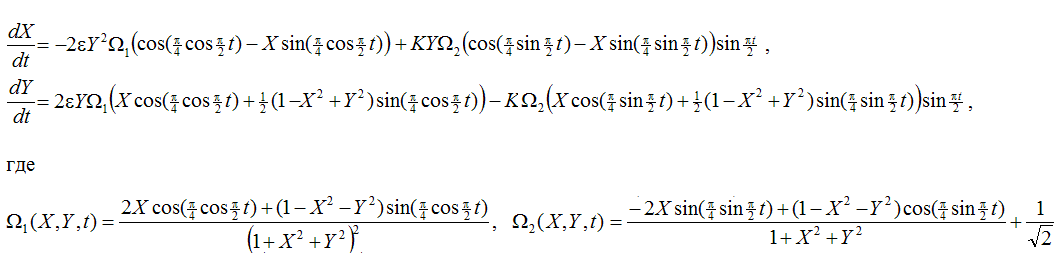
Подобрав параметры, например, K=1.9, e=0.72, получаем аттрактор, представленный на рисунке в трехмерном расширенном фазовом пространстве неавтономной системы. В сечении плоскостью t=const можно видеть объект, аналогичный аттрактору рассмотренного выше отображения. Компьютерная проверка критерия конусов для модифицированной системы подтверждает гиперболическую природу аттрактора.
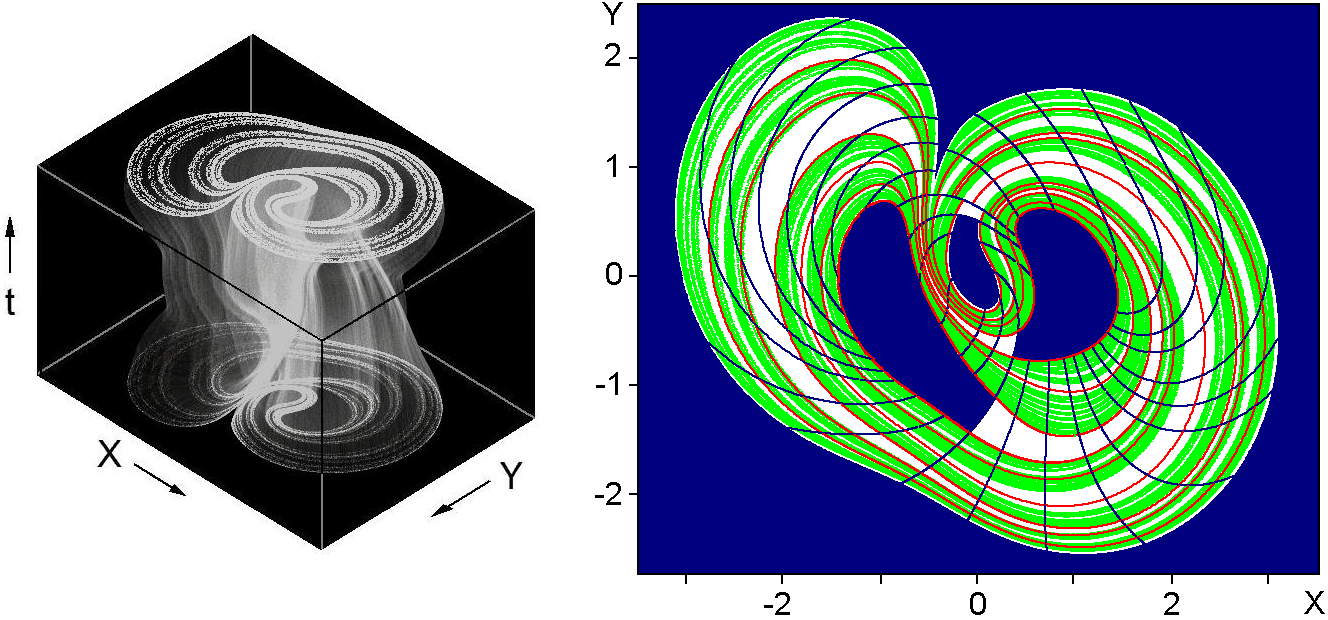
Еще одним свидетельством гиперболичности служит построенная на основе численных расчетов картина расположения многообразий на плоскости (X,Y) в сечении Пуанкаре. Область, содержащая аттрактор, показана светлым тоном, а сам аттрактор зеленым цветом. Неустойчивые многообразия показаны красным и располагаются вдоль волокон аттрактора, а устойчивые, показанные черным, – поперек структуры волокон. Видно, что в области, содержащей аттрактор, характер взаимного расположения многообразий исключает ситуацию касания.
На диаграмме внизу приведены зависимости показателей Ляпунова от одного параметра задачи при другом фиксированном, и указаны интервалы по параметру, в которых, согласно расчетам, аттрактор гиперболический.
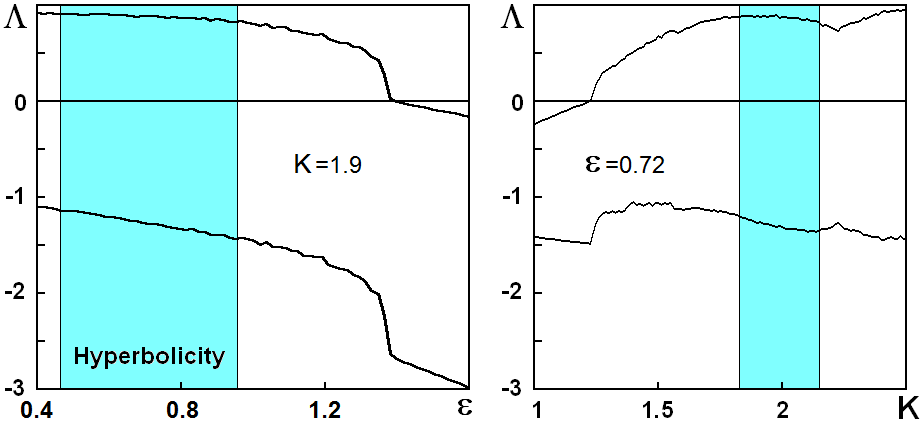
Надо подчеркнуть, что это, по-видимому, первый представленный в явном виде пример неавтономной системы с гладкими коэффициентами,
имеющей аттрактор Плыкина в сечении Пуанкаре, притом
с минимально возможной размерностью фазового пространства.
Так как уравнения достаточно громоздкие, естественно спросить, а есть ли реальная возможность получить
динамику такого типа в каком-либо физическом устройстве?
Это можно сделать на базе системы двух связанных неавтономных осцилляторов, как объясняется далее.
(Но размерность фазового пространства получается выше!)
| Аттрактор типа Плыкина в связанных осцилляторах |
Обратимся сначала к системе двух связанных элементов, совершающих автоколебания при компенсации потерь из общего источника энергии, так что уравнения для комплексных амплитуд a и b имеют вид
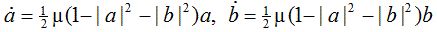
где m - параметр. В установившемся режиме сумма квадратов модулей амплитуд равна единице, и мгновенные состояния допускают представление точками единичной сферы, если игнорировать общий фазовый множитель. Для этого полагаем
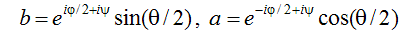
и считаем, что прямоугольные координаты точки на сфере выражаются через угловые переменные обычным соотношением
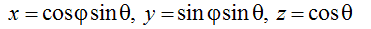
Рассмотрим такое же отображение сферы в себя, как и раньше, но представим его теперь в шесть стадий для удобства построения. Стадии 1 и 2 такие же, как и раньше. Стадии 4 и 5 такие же, как 1 и 2, но с противоположным направлением вращения. Дополнительные стадии 3 и 6 отвечают просто повороту сферы вокруг оси y на 90о. Проводимые преобразования иллюстрируются рисунком, где приводятся также уравнения, которым должны удовлетворять комплексные амплитуды a и b на каждой стадии. Ответственные за автоколебания члены считаем включенными только на стадиях поворота, что упрощает вывод отображения Пуанкаре.

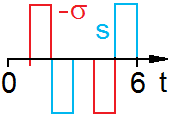
Вводя коэффициенты s и s,
зависящие от времени кусочно-непрерывным образом
и принимающие значения
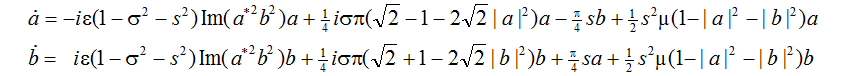
|
|
Отображение Пуанкаре, задающее трансформацию состояния за период T=6, можно получить в явной форме. Пусть начальные условия для комплексных амплитуд в момент t=nT отвечают вектору состояния Xn=(an, bn). Отображение Пуанкаре представим как композицию отображений за полпериода:
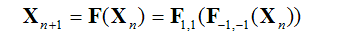
где отображение Fs,s определяется формулами
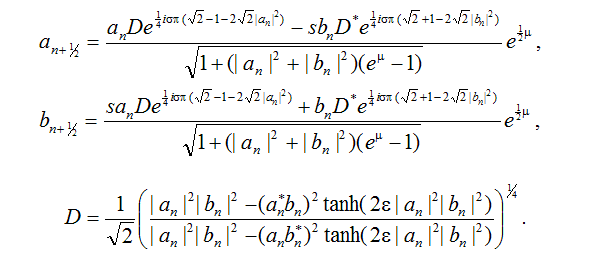
На рисунке показан в представлении на сфере аттрактор этого отображения при e=1 и m=1. Он не отличается от рассмотренного выше, в первом разделе настоящей страницы. А вот эволюция структуры в непрерывном времени другая, поскольку последовательность преобразований в пределах периода сформулирована иначе.

|

|
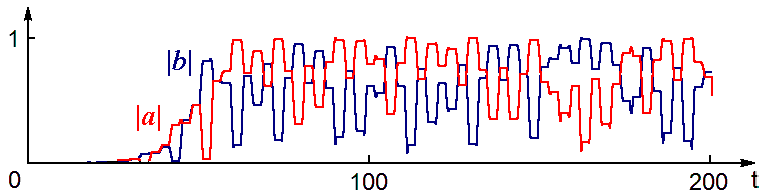
Далее приводятся некоторые численные результата, относящиеся к рассматриваемой системе связанных осцилляторов. Представлены зависимости амплитуд двух осцилляторов от времени в переходном процессе, который завершается установлением хаотического режима.
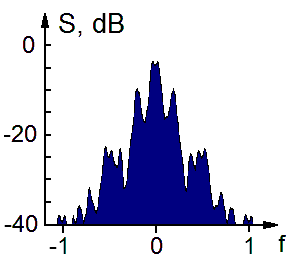
Показаны также спектр колебаний одного из осцилляторов в установившемся режиме и фазовый портрет, где в горизонтальной плоскости отложены угловые координаты на сфере, а по вертикальной оси - время в пределах одного периода изменения коэффициентов в уравнениях. Картинка вызывает ассоцииации с поднимающимся и клубящимся дымом.
|

|
Строго говоря, в системе уравнений для комплексных амплитуд аттрактор не может интерпретироваться как однородно гиперболический из-за наличия нейтрального направления в пространстве состояний, отвечающего общей фазе. Он должен быть отнесен к классу частично гиперболических аттракторов. Для модели, исследуемой здесь, данное замечание носит формальный характер, поскольку инвариантность по отношению к сдвигу фазы точная, а с точки зрения остальных переменных (амплиитуд и относительной фазы) динамика такая же, как в случае настоящего гиперболического аттрактора. Однако в системах, для которых представление посредством медленных комплексных амплитуд будет приближенным способом описания, следует ожидать появления специфики, определяемой природой частично гиперболического аттрактора. По-видимому, если поправки, обусловленные отклонением от приближенного описания невелики, то общая фаза будет совершать медленное случайное блуждание, тогда как динамика остальных переменных сохранит свой характер.
Поскольку системы связанных осцилляторов встречаются во многих областях физики и техники, естественно думать, что предложенная модель может допускать реализацию на их основе. Сказанное относится, в частности, к электронным устройствам, механическим системам, объектам лазерной физики и нелинейной оптики. Системы с гиперболическим хаосом могут оказаться интересными для приложений в особенности благодаря присущему им свойству грубости или структурной устойчивости, что будет означать нечувствительность устройств к вариации параметров, характеристик составных элементов, техническим флуктуациям и шумам и т.п.
Конкретный пример электронной схемы, где реализуется аттрактор Плыкина, представлен в работе [4].
ЛИТЕРАТУРА
[1] С.П. Кузнецов. Пример неавтономной системы с непрерывным временем, имеющей аттрактор типа Плыкина в отображении Пуанкаре. Нелинейная динамика, 5, 2009, №3, 403-424.
![]()
[2] S.P. Kuznetsov. A non-autonomous flow system with Plykin type attractor. Communications in Nonlinear Science and Numerical Simulation, 14, 2009, 3487–3491.
![]()
[3] S.P. Kuznetsov. Plykin-type attractor in nonautonomous coupled oscillators. CHAOS, 19, 2009, No 1, 013114.
![]()
[4] S.P. Kuznetsov. Plykin type attractor in electronic device simulated in MULTISIM. CHAOS, 21, 2011, 043105.
![]()